Bài 1.16 trang 19 SGK Toán 11 tập 1 là một bài tập quan trọng trong chương trình học Toán 11, tập trung vào việc xác định tập xác định của hàm số. Bài tập này yêu cầu học sinh nắm vững kiến thức về điều kiện xác định của các phép toán và hàm số cơ bản.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cùng với phương pháp giải bài tập này, giúp bạn hiểu rõ bản chất và áp dụng vào các bài tập tương tự.
Một vận động viên bắn súng nằm trên mặt đất để ngắm bắn các mục tiêu khác nhau trên một bức tường thẳng đứng. Vận động viên bắn trúng một mục tiêu cách mặt đất 20 m tại một góc ngắm (góc hợp bởi phương bắn và phương ngang).
Đề bài
Một vận động viên bắn súng nằm trên mặt đất để ngắm bắn các mục tiêu khác nhau trên một bức tường thẳng đứng. Vận động viên bắn trúng một mục tiêu cách mặt đất 20 m tại một góc ngắm (góc hợp bởi phương bắn và phương ngang). Nếu tăng góc ngắm đó lên hai lần thì vận động viên bắn trúng một mục tiêu cách mặt đất 45 m. Tính khoảng cách từ vận động viên đến bức tường.
Phương pháp giải - Xem chi tiết
Áp dụng tỉ số lượng giác:
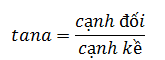
Và công thức nhân đôi.
Lời giải chi tiết
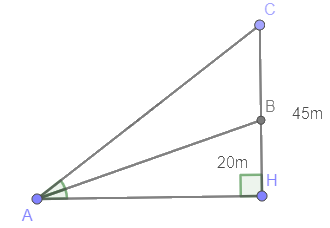
Gọi A là vị trí vận động viên nằm, B là mục tiêu cách mặt đất 20m, C là mục tiêu cách mặt đất 45m và H như trên hình
\(\begin{array}{l}\tan \widehat {BAH} = \frac{{BH}}{{AH}} = \frac{{20}}{{AH}}\\\tan \widehat {CAH} = \frac{{CH}}{{AH}} = \frac{{45}}{{AH}}\\\widehat {CAH} = 2\widehat {BAH}\\ \Rightarrow \tan \left( {2.\widehat {BAH}} \right) = \frac{{45}}{{AH}}\\ \Leftrightarrow \frac{{2\tan \widehat {BAH}}}{{1 - {{\tan }^2}\widehat {BAH}}} = \frac{{45}}{{AH}}\\ \Leftrightarrow \left( {2.\frac{{20}}{{AH}}} \right):\left[ {1 - {{\left( {\frac{{20}}{{AH}}} \right)}^2}} \right] = \frac{{45}}{{AH}}\\ \Leftrightarrow \frac{{40}}{{AH}}:\left( {1 - \frac{{400}}{{A{H^2}}}} \right) = \frac{{45}}{{AH}}\\ \Leftrightarrow \frac{{40}}{{AH}}:\frac{{A{H^2} - 400}}{{A{H^2}}} = \frac{{45}}{{AH}}\\ \Leftrightarrow \frac{{40}}{{AH}}.\frac{{A{H^2}}}{{A{H^2} - 400}} = \frac{{45}}{{AH}}\\ \Leftrightarrow \frac{{40AH}}{{A{H^2} - 400}} = \frac{{45}}{{AH}}\\ \Leftrightarrow 40A{H^2} = 45A{H^2} - 18000\\ \Leftrightarrow A{H^2} = 3600\\ \Rightarrow AH = 60\end{array}\)
Bài 1.16 SGK Toán 11 tập 1 yêu cầu xác định tập xác định của các hàm số sau:
Hàm số a) y = \frac{1}{x-2}
Để hàm số y xác định, mẫu số x-2 phải khác 0. Do đó, x ≠ 2. Vậy tập xác định của hàm số là D = ℝ \ {2}.
Hàm số b) y = \sqrt{x+3}
Để hàm số y xác định, biểu thức dưới dấu căn phải lớn hơn hoặc bằng 0. Do đó, x+3 ≥ 0, suy ra x ≥ -3. Vậy tập xác định của hàm số là D = [-3, +∞).
Hàm số c) y = \frac{x+1}{\sqrt{x-1}}
Để hàm số y xác định, cần có hai điều kiện: mẫu số khác 0 và biểu thức dưới dấu căn phải lớn hơn 0. Do đó, x-1 > 0, suy ra x > 1. Vậy tập xác định của hàm số là D = (1, +∞).
Hàm số d) y = \frac{2x-1}{x^2 - 4}
Để hàm số y xác định, mẫu số phải khác 0. Do đó, x^2 - 4 ≠ 0, suy ra x ≠ 2 và x ≠ -2. Vậy tập xác định của hàm số là D = ℝ \ {-2, 2}.
Để giải các bài tập về tập xác định của hàm số, cần nắm vững các quy tắc sau:
Hàm số phân thức: Mẫu số khác 0.
Hàm số chứa căn thức bậc chẵn: Biểu thức dưới dấu căn lớn hơn hoặc bằng 0.
Hàm số chứa logarit: Điều kiện xác định của logarit phải được thỏa mãn (cơ số lớn hơn 0 và khác 1, biểu thức bên trong logarit lớn hơn 0).
Khi gặp một hàm số phức tạp, cần phân tích cấu trúc của hàm số và áp dụng các quy tắc trên một cách linh hoạt. Việc kết hợp các điều kiện xác định bằng các phép toán logic (và, hoặc) là rất quan trọng.
Ví dụ 1: Xác định tập xác định của hàm số y = \frac{1}{\sin x}
Hàm số y xác định khi \sin x ≠ 0, tức là x ≠ kπ, với k ∈ ℤ. Vậy tập xác định của hàm số là D = ℝ \ {kπ, k ∈ ℤ}.
Ví dụ 2: Xác định tập xác định của hàm số y = \log_2(x-1)
Hàm số y xác định khi x-1 > 0, suy ra x > 1. Vậy tập xác định của hàm số là D = (1, +∞).
Để củng cố kiến thức, bạn có thể tự giải các bài tập sau:
Bài 1.17 trang 19 SGK Toán 11 tập 1
Bài 1.18 trang 19 SGK Toán 11 tập 1
Việc luyện tập thường xuyên sẽ giúp bạn nắm vững kiến thức và kỹ năng giải bài tập về tập xác định của hàm số.
Hy vọng với lời giải chi tiết và phương pháp giải bài tập Bài 1.16 trang 19 SGK Toán 11 tập 1, các bạn học sinh sẽ hiểu rõ hơn về chủ đề này và đạt kết quả tốt trong học tập. Hãy truy cập giaitoan.edu.vn để khám phá thêm nhiều bài giải và tài liệu học tập hữu ích khác.