Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 1 tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Ở bài viết này, chúng ta sẽ cùng nhau giải quyết các bài tập trong mục 3 trang 69, 70, 71, 72, 73 SGK Toán 11 tập 1. Hãy cùng bắt đầu!
Cho hàm số \(y = f(x) = \frac{1}{x}\)
Cho hàm số \(y = f(x) = \frac{1}{x}\)
a, Tìm tập xác định của hàm số.
b, Tính giá trị của hàm số tại các điểm trong bảng giá trị sau:
c, Nhận xét gì về giá trị của f(x) khi x dần đến \( + \infty \)? Khi x dần đến \( - \infty \)?
Phương pháp giải:
Tập xác định là các giá trị của x để hàm số có nghĩa.
Thay giá trị của x vào hàm số để được các giá trị của f(x) tương ứng.
Lời giải chi tiết:
a, Tập xác định: R\{0}.
b, Thay lần lượt các giá trị của x vào f(x) ta được:
\(\)x dần đến \( - \infty \) thì f(x)=0
\(f( - {10^8}) = \frac{1}{{ - {{10}^8}}} = - {10^{ - 8}}\)
\(f(10) = \frac{1}{{10}}\)
\(f( - {10^3}) = \frac{1}{{ - {{10}^3}}} = - {10^{ - 3}}\)
\(f(1000) = \frac{1}{{1000}} = {10^{ - 3}}\)
\(f( - {10^2}) = \frac{1}{{ - {{10}^2}}} = - {10^{ - 2}}\)
\(f(100000) = \frac{1}{{100000}} = {10^{ - 5}}\)
\(f( - 10) = \frac{1}{{ - 10}} = \frac{{ - 1}}{{10}}\)
\(f({10^9}) = \frac{1}{{{{10}^9}}} = {10^{ - 9}}\)
x dần đến \( + \infty \) thì f(x)=0.

c, Khi x dần đến và x dần đến thì f(x)=0.
Cho hàm số \(f(x) = \frac{{\sqrt {{x^2} + 1} }}{x}\). Tìm \(\mathop {\lim }\limits_{x \to - \infty } f(x)\) và \(\mathop {\lim }\limits_{x \to + \infty } f(x)\).
Phương pháp giải:
Đưa x ra khỏi dấu căn để chia cả tử và mẫu cho x.
Với x dần đến \( - \infty \) thì |x| = -x
Với x dần đến \( + \infty \) thì |x| = x.
Lời giải chi tiết:
Hàm số có tập xác định là \(( - \infty ;0) \cup (0; + \infty )\)
Giả sử \(({x_n})\) là một dãy số bất kì thỏa mãn \({x_n} < 0\) và \(\lim {x_n} = - \infty \)
Ta có \(\lim f({x_n}) = \frac{{\sqrt {x_n^2 + 1} }}{{{x_n}}} = \lim \frac{{\left| {{x_n}} \right|.\sqrt {1 + \frac{1}{{x_n^2}}} }}{{{x_n}}} = \lim \frac{{ - {x_n}.\sqrt {1 + \frac{1}{{x_n^2}}} }}{{{x_n}}} = \lim ( - \sqrt {1 + \frac{1}{{x_n^2}}} ) = - 1\)
Giả sử \(({x_n})\) là một dãy số bất kì thỏa mãn \({x_n} > 0\) và \(\lim {x_n} = + \infty \)
Ta có \(\lim f({x_n}) = \frac{{\sqrt {x_n^2 + 1} }}{{{x_n}}} = \lim \frac{{\left| {{x_n}} \right|.\sqrt {1 + \frac{1}{{x_n^2}}} }}{{{x_n}}} = \lim \frac{{{x_n}.\sqrt {1 + \frac{1}{{x_n^2}}} }}{{{x_n}}} = \lim \sqrt {1 + \frac{1}{{x_n^2}}} = 1\)
Vậy \(\mathop {\lim }\limits_{x \to - \infty } f(x) = - 1\) và \(\mathop {\lim }\limits_{x \to + \infty } f(x) = 1\).
Tìm \(\mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {{x^2} - 4} }}{{x + 5}}\).
Phương pháp giải:
Đưa x ra khỏi dấu căn để chia cả tử và mẫu cho x.
Với x dần đến \( - \infty \) thì |x| = -x
Lời giải chi tiết:
Hàm số có tập xác định là \(( - \infty ; - 5) \cup ( - 5; + \infty )\)
Ta có: \(\mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {{x^2} - 4} }}{{x + 5}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{\left| x \right|.\sqrt {1 - \frac{4}{{{x^2}}}} }}{{x + 5}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - x\sqrt {1 - \frac{4}{{{x^2}}}} }}{{x + 5}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - \sqrt {1 - \frac{4}{{{x^2}}}} }}{{1 + \frac{5}{x}}}\)
Vì \(\mathop {\lim }\limits_{x \to - \infty } - \sqrt {1 - \frac{4}{{{x^2}}}} = - 1\) , lim 1=1 và \(\mathop {\lim }\limits_{x \to - \infty } \frac{5}{x} = 0\) ta có:
\(\mathop {\lim }\limits_{x \to - \infty } \frac{{ - \sqrt {1 - \frac{4}{{{x^2}}}} }}{{1 + \frac{5}{x}}} = - 1\).
Cho hàm số \(f(x) = {x^2}\) và dãy số \(({x_n})\) với \({x_n} = n + 1\)
a, Tìm \({\mathop{\rm l}\nolimits} {\rm{im }}{{\rm{x}}_n}\)
b, Tính \(f({x_n})\) theo n và tìm \({\mathop{\rm l}\nolimits} {\rm{im f(}}{{\rm{x}}_n})\).
Phương pháp giải:
a, Thay \({x_n} = n + 1\) để tìm \({\mathop{\rm l}\nolimits} {\rm{im }}{{\rm{x}}_n}\)
b, Thay \({x_n} = n + 1\) vào hàm số \(f(x) = {x^2}\) để tìm \(f({x_n})\)
Dựa vào câu a để xác định \({\mathop{\rm l}\nolimits} {\rm{im f(}}{{\rm{x}}_n})\).
Lời giải chi tiết:
a, Ta có: \({\mathop{\rm l}\nolimits} {\rm{im }}{{\rm{x}}_n} = \lim (n + 1)\)
\(\mathop {\lim }\limits_{n \to - \infty } (n + 1) = - \infty \) và \(\mathop {\lim }\limits_{n \to + \infty } (n + 1) = + \infty \).
b, Thay \({x_n} = n + 1\) vào hàm số \(f(x) = {x^2}\) ta được:
\(f({x_n}) = {(n + 1)^2}\)
\(\mathop {\lim }\limits_{n \to - \infty } {\rm{f(}}{{\rm{x}}_n}) = \mathop {\lim }\limits_{n \to - \infty } {(n + 1)^2} = + \infty \) và \(\mathop {\lim }\limits_{n \to + \infty } {\rm{f(}}{{\rm{x}}_n}) = \mathop {\lim }\limits_{n \to + \infty } {(n + 1)^2} = + \infty \).
Tìm \(\mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2} + 1}}{x}\)
Phương pháp giải:
Chia tử cho mẫu để tính giới hạn
Lời giải chi tiết:
Hàm số \(f(x) = \frac{{{x^2} + 1}}{x} = x + \frac{1}{x}\) có tập xác định là \(( - \infty ;0) \cup (0; + \infty )\)
\(\forall ({x_n}),{x_n} < 0\)và \({\mathop{\rm l}\nolimits} {\rm{im }}{{\rm{x}}_n} = - \infty \), ta có \(\lim f({x_n}) = \lim ({x_n} + \frac{1}{{{x_n}}}) = {\mathop{\rm l}\nolimits} {\rm{im }}{{\rm{x}}_n}(1 + \frac{1}{{x_n^2}})\)
Vì \({\mathop{\rm l}\nolimits} {\rm{im x}}_n^2 = + \infty \) nên \(\lim \frac{1}{{x_n^2}} = 0\). Suy ra \(\lim (1 + \frac{1}{{x_n^2}}) = 1\)
Vì \({\mathop{\rm l}\nolimits} {\rm{im }}{{\rm{x}}_n} = - \infty \) và \(\lim (1 + \frac{1}{{x_n^2}}) = 1\) nên \({\mathop{\rm l}\nolimits} {\rm{im }}{{\rm{x}}_n}(1 + \frac{1}{{x_n^2}}) = - \infty \)
Vậy \(\mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2} + 1}}{x} = - \infty \).
Cho hàm số \(f(x) = \frac{{x - 1}}{{x + 1}}\) và g(x)=x+1
a, Tìm \(\mathop {\lim }\limits_{x \to + \infty } f(x)\) và \(\mathop {\lim }\limits_{x \to + \infty } g(x)\)
b, Tìm \(\mathop {\lim }\limits_{x \to + \infty } {\rm{[}}f(x).g(x){\rm{]}}\).
Phương pháp giải:
a, Với f(x) chia tử cho mẫu để tìm giới hạn
Với g(x) thì \(\mathop {\lim }\limits_{x \to + \infty } g(x) = \mathop {\lim }\limits_{x \to + \infty } (x + 1) = + \infty \)
b, Tính f(x). g(x) và dựa vào câu a xác định \(\mathop {\lim }\limits_{x \to + \infty } {\rm{[}}f(x).g(x){\rm{]}}\)
Lời giải chi tiết:
a, Hàm số \(f(x) = \frac{{x - 1}}{{x + 1}} = 1 - \frac{2}{{x + 1}}\) có tập xác định \(( - \infty , - 1) \cup ( - 1; + \infty )\)
\(\mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to + \infty } (1 - \frac{2}{{x + 1}}) = 1\)
\(\mathop {\lim }\limits_{x \to + \infty } g(x) = \mathop {\lim }\limits_{x \to + \infty } (x + 1) = + \infty \)
b, Ta có: \(f(x).g(x) = \frac{{x - 1}}{{x + 1}}.(x + 1) = x - 1\)
\(\mathop {\lim }\limits_{x \to + \infty } f(x).g(x) = \mathop {\lim }\limits_{x \to + \infty } (x - 1) = + \infty \).
Tìm \(\mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{{\sqrt {{x^2} + 2x} }}\).
Phương pháp giải:
Xác định \(\mathop {\lim }\limits_{x \to {0^ + }} \sqrt {{x^2} + 2x} \) để tìm \(\mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{{\sqrt {{x^2} + 2x} }}\)
Lời giải chi tiết:
\(\mathop {\lim }\limits_{x \to {0^ + }} \sqrt {{x^2} + 2x} \)=0 và \(\sqrt {{x^2} + 2x} > 0,\forall x > 0\) nên \(\mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{{\sqrt {{x^2} + 2x} }} = + \infty \).
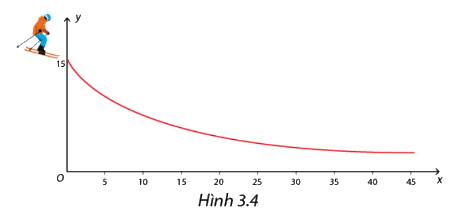
Trong một cuộc thi các môn thể thao trên tuyết, người ta muốn thiết kế một đường trượt bằng bang cho nội dung đổ dốc tốc độ đường dài

Vận động viên sẽ xuất phát từ vị trí (0; 15) cao 15 m so với mặt đất (trục 0x) . Đường trượt phải thỏa mãn yêu cầu là càng ra xa thì càng gần mặt đất để tiết kiệm lượng tuyết nhân tạo. Một nhà thiết kế đề nghị sử dụng đường cong là đồ thị \(y = f(x) = \frac{{150}}{{x + 10}}\) với \(x \ge 0\). Hãy kiểm tra xem hàm số y=f(x) có thỏa mãn các điều kiện dưới đây hay không:
a, Có đồ thị đi qua điểm (0,15)
b, Giảm trên \(\left[ {0, + \infty } \right]\)
c, Càng ra xa ( x càng lớn), đồ thị càng gần trục Ox với khoảng cách nhỏ tùy ý.
Phương pháp giải:
a, Thay tọa độ (0,15) vào hàm số để kiểm tra điểm có thuộc hàm số hay không?
b, Nhận xét với x càng tăng thì giá trị f(x) càng giảm
c, Tính lim f(x) khi x dần đến \( + \infty \)
Lời giải chi tiết:
a, Thay x=0 vào hàm số \(y = f(x) = \frac{{150}}{{x + 10}}\) ta được:
\(y = \frac{{150}}{{0 + 10}} = \frac{{150}}{{10}} = 15\)
Vậy điểm (0,15) thuộc đồ thị hàm số.
b, Nhận thấy khi x càng tăng thì giá trị hàm số càng giảm. Vậy hàm số \(y = f(x) = \frac{{150}}{{x + 10}}\) giảm trên \(\left[ {0, + \infty } \right]\)
c, Ta có : \(\mathop {\lim }\limits_{x \to + \infty } \frac{{150}}{{x + 10}} = 0\)
Vậy càng ra xa ( x càng lớn), đồ thị càng gần trục Ox với khoảng cách nhỏ tùy ý.
Mục 3 của SGK Toán 11 tập 1 thường tập trung vào các chủ đề quan trọng như phép biến hình, vectơ, và các ứng dụng của chúng trong hình học. Việc nắm vững kiến thức trong mục này là nền tảng cho việc học các chương tiếp theo và giải quyết các bài toán phức tạp hơn.
Mục 3 thường bao gồm các nội dung sau:
Dưới đây là giải chi tiết các bài tập trong mục 3, trang 69, 70, 71, 72, 73 SGK Toán 11 tập 1:
Đề bài: Cho điểm A(1; 2). Tìm ảnh của điểm A qua phép tịnh tiến theo vectơ v = (3; -1).
Giải: Gọi A'(x'; y') là ảnh của điểm A qua phép tịnh tiến theo vectơ v. Ta có:
x' = x + vx = 1 + 3 = 4
y' = y + vy = 2 + (-1) = 1
Vậy A'(4; 1).
Đề bài: Cho đường thẳng d: x + 2y - 3 = 0. Tìm ảnh của đường thẳng d qua phép đối xứng trục Ox.
Giải: Phép đối xứng trục Ox biến điểm M(x; y) thành điểm M'(x; -y). Do đó, ảnh của đường thẳng d qua phép đối xứng trục Ox là đường thẳng d': x + 2(-y) - 3 = 0, hay x - 2y - 3 = 0.
Đề bài: Cho điểm B(-2; 3). Tìm ảnh của điểm B qua phép đối xứng tâm I(1; -1).
Giải: Gọi B'(x'; y') là ảnh của điểm B qua phép đối xứng tâm I. Ta có:
x' = 2xi - x = 2(1) - (-2) = 4
y' = 2yi - y = 2(-1) - 3 = -5
Vậy B'(4; -5).
Đề bài: Cho tam giác ABC với A(0; 0), B(1; 2), C(-1; 4). Tìm ảnh của tam giác ABC qua phép quay tâm O(0; 0) góc 90 độ.
Giải: Gọi A', B', C' lần lượt là ảnh của A, B, C qua phép quay tâm O góc 90 độ. Ta có:
A'(0; 0)
B'(-2; 1)
C'(-4; -1)
Vậy ảnh của tam giác ABC là tam giác A'B'C' với A'(0; 0), B'(-2; 1), C'(-4; -1).
Đề bài: Chứng minh rằng phép tịnh tiến và phép đối xứng trục là các phép biến hình.
Giải: (Chứng minh dựa trên định nghĩa của phép biến hình, đảm bảo bảo toàn khoảng cách giữa các điểm).
Để giải tốt các bài tập về phép biến hình, các em cần:
Hy vọng với lời giải chi tiết và những lời khuyên trên, các em sẽ tự tin hơn trong việc giải các bài tập về phép biến hình trong SGK Toán 11 tập 1. Chúc các em học tốt!
Lưu ý: Bài giải trên chỉ mang tính chất tham khảo. Các em nên tự mình suy nghĩ và giải bài tập để hiểu rõ hơn về kiến thức.