Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 của giaitoan.edu.vn. Ở đây, chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho tất cả các bài tập trong SGK, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Mục 2 của chương trình Toán 11 tập 2 thường tập trung vào các kiến thức quan trọng về... (Nội dung cụ thể của Mục 2 sẽ được điền vào đây khi có thông tin chi tiết)
Quan sát khối rubik hình lập phương (Hình 8.33).
Quan sát khối rubik hình lập phương (Hình 8.33).
a) Hãy tính số đo của các góc nhị diện tạo bởi mặt đỏ và mặt xanh; mặt trắng và mặt xanh; mặt trắng và mặt đỏ.
b) Có hay không một đường thẳng a nằm trong mặt xanh và vuông góc với mặt đỏ?
Phương pháp giải:
Quan sát hình vẽ.
Lời giải chi tiết:
a) Số đo giữa các góc nhị diện tạo bởi mặt đỏ và mặt xanh, mặt trắng và mặt xanh, mặt trắng và mặt đỏ đều bằng \({90^0}\).
b) Có đường thẳng nằm trong mặt xanh và vuông góc với mặt đỏ.
Đặt cây bút chì d vuông góc với mặt bàn \(\left( \alpha \right)\) và đặt một tấm bia cứng hình chữ nhật \(\left( \beta \right)\) sao cho thân bút chì nằm trong tấm bìa (Hình 8.34). Ta có hình ảnh đường thẳng d vuông góc với mặt phẳng \(\left( \alpha \right)\) và mặt phẳng \(\left( \beta \right)\) chứa d. Gọi a là giao tuyến của \(\left( \alpha \right)\) và \(\left( \beta \right)\). Qua giao điểm O của a và d, vẽ một dường thẳng d’ nằm trong \(\left( \alpha \right)\) và vuông góc với a. Hai mặt phẳng \(\left( \alpha \right)\)và \(\left( \beta \right)\) có vuông góc nhau không? Vì sao?

Phương pháp giải:
2 mặt phẳng vuông góc với nhau nếu một trong bốn nhị diện được tạo bởi 2 mặt vuông góc với nhau.
Lời giải chi tiết:
Hai mặt phẳng \(\left( \alpha \right)\)và \(\left( \beta \right)\) có vuông góc nhau. Vì nhị diện tạo bởi 2 mặt phẳng này là nhị diện vuông.
Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right)\) và tam giác ABC vuông tại B. Tìm các cặp mặt phẳng vuông góc với nhau.

Phương pháp giải:
Hai mặt phẳng vuông góc với nhau nếu mặt phẳng này có chứa một đường thẳng vuông góc với mặt phẳng kia.
Lời giải chi tiết:
\(SA \bot \left( {ABC} \right)\) nên (SAB), (SAC) vuông góc với (ABC).
AB vuông góc với AC, SA vuông góc với AB nên AB vuông góc với (SAC)
Suy ra (SAB) và (SAC) vuông góc với nhau.
Trong phòng khách của một căn nhà, bức tường và nền nhà vuông góc nhau. Họa sĩ về một hàng cây trên bức tường với thân cây vuông góc với gờ của mảng gỗ ép sát bức tường (Hình 8.37). Các cây này có vuông góc với nền nhà không? Vì sao?

Phương pháp giải:
Đường thẳng d vuông góc với (P) nếu d vuông góc với 2 đường thẳng cắt nhau thuộc (P).
Lời giải chi tiết:
Các cây này có vuông góc với nền nhà. Vì các cây vuông góc với mép tường và các đường kẻ trên nền.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Chứng minh tam giác SCD cân tại S.
Phương pháp giải:
Cho 2 mặt phẳng vuông góc với nhau, mỗi đường thẳng nằm trong mặt phẳng này và vuông góc với giao tuyến đều vuông góc với mặt phẳng kia.
Chứng minh: SC = SD.
Lời giải chi tiết:

Gọi E là trung điểm của AB nên SE vuông góc với AB
Suy ra SE vuông góc với (ABCD)
\( \Rightarrow \)SE vuông góc với ED, EC nên tam giác SED vuông tại E, tam giác SEC vuông tại E
ABCD là hình vuông nên AB vuông góc với AD, BD. Suy ra tam giác AEB vuông tại A, BEC vuông tại B
Ta có: \(SD = \sqrt {S{E^2} + E{D^2}} = \sqrt {S{E^2} + A{E^2} + A{D^2}} \)
\(SC = \sqrt {S{E^2} + E{C^2}} = \sqrt {S{E^2} + B{E^2} + B{C^2}} \)
Mà: AE = BE, AD = BC nên SD = SC
Suy ra SCD cân tại S.
Cho hai mặt phẳng \(\left( \alpha \right)\), \(\left( \beta \right)\) cắt nhau theo giao tuyến d và cùng vuông góc với mặt phẳng \(\left( \gamma \right)\). A là một điểm chung của \(\left( \alpha \right)\) và \(\left( \beta \right)\). Gọi a là đường thẳng qua A và vuông góc \(\left( \gamma \right)\).
a) a có thuộc mặt phẳng \(\left( \alpha \right)\) không? Vì sao?
b) a có thuộc mặt phẳng \(\left( \beta \right)\) không? Vì sao?
c) Từ đó, có kết luận gì về quan hệ giữa d và \(\left( \gamma \right)\).

Phương pháp giải:
2 đường thẳng cùng vuông góc với một mặt phẳng thì song song hoặc trùng nhau.
Lời giải chi tiết:
a) a và d cùng vuông góc với \(\left( \gamma \right)\). Suy ra a và d trùng nhau hoặc song song với nhau.
Mà A là điểm chung của \(\left( \alpha \right)\) và \(\left( \beta \right)\). Suy ra A phải thuộc d.
Mặt khác, A cũng thuộc a. Suy ra a chính là đường thẳng d.
b) a và đường thẳng d nên a thuộc \(\left( \beta \right)\)
c) a chính là d. Suy ra d vuông góc với \(\left( \gamma \right)\).
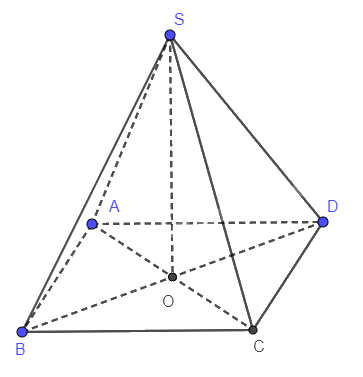
Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng (ABCD). Chứng minh rằng \(\left( {SAC} \right) \bot \left( {SBD} \right)\).
Phương pháp giải:
Nếu 2 mặt phẳng cắt nhau và cùng vuông góc với một mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba.
Nếu một đường thẳng vuông góc với 2 đường thẳng cắt nhau cùng nằm trong một mặt phẳng thì nó vuông góc với mặt phẳng ấy.
Lời giải chi tiết:

\(\left\{ \begin{array}{l}\left( {SAC} \right) \bot \left( {ABCD} \right)\\\left( {SBD} \right) \bot \left( {ABCD} \right)\\\left( {SAC} \right) \cap \left( {SBD} \right) = SO\end{array} \right. \Rightarrow SO \bot \left( {ABCD} \right)\)
\( \Rightarrow SO \bot BD\)
Mà: \(AC \bot BD\)
\( \Rightarrow \left( {SAC} \right) \bot BD\)
\( \Rightarrow \left( {SAC} \right) \bot \left( {SBD} \right)\)
Mục 2 trong SGK Toán 11 tập 2 thường xoay quanh các chủ đề về đạo hàm của hàm số, bao gồm các khái niệm cơ bản, quy tắc tính đạo hàm, và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế. Việc nắm vững kiến thức trong mục này là vô cùng quan trọng, vì nó là nền tảng cho các kiến thức nâng cao hơn trong chương trình học.
Các bài tập trên trang 65 thường tập trung vào việc kiểm tra sự hiểu biết của học sinh về định nghĩa đạo hàm, ý nghĩa hình học và vật lý của đạo hàm. Học sinh cần nắm vững các công thức tính đạo hàm cơ bản và áp dụng chúng để giải quyết các bài toán đơn giản.
Trang 66 giới thiệu các quy tắc tính đạo hàm của tổng, hiệu, tích, thương của các hàm số, cũng như quy tắc đạo hàm của hàm hợp. Các bài tập trên trang này yêu cầu học sinh phải thành thạo các quy tắc này và biết cách áp dụng chúng một cách linh hoạt.
Các bài tập trên trang 67 tập trung vào việc tính đạo hàm của các hàm số lượng giác cơ bản như sin, cos, tan, cot. Học sinh cần nhớ các công thức đạo hàm của các hàm số này và biết cách sử dụng chúng để giải quyết các bài toán phức tạp hơn.
Trang 68 là nơi tổng hợp các bài tập về đạo hàm, bao gồm cả các bài tập về khái niệm, quy tắc tính đạo hàm, và đạo hàm của các hàm số lượng giác. Các bài tập trên trang này thường có độ khó cao hơn và yêu cầu học sinh phải có khả năng tư duy logic và sáng tạo.
Đạo hàm có rất nhiều ứng dụng trong thực tế, chẳng hạn như:
Để học tốt môn Toán 11, đặc biệt là phần đạo hàm, các em cần:
Hy vọng rằng với những kiến thức và phương pháp giải bài tập được trình bày trong bài viết này, các em sẽ tự tin hơn trong việc học tập và giải quyết các bài toán về đạo hàm trong SGK Toán 11 tập 2. Chúc các em học tốt!