Bài 3.10 trang 74 SGK Toán 11 tập 1 là một bài tập quan trọng trong chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng giải bài toán liên quan đến vectơ. Bài tập này yêu cầu học sinh vận dụng kiến thức về tích vô hướng của hai vectơ để giải quyết các vấn đề thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu và phương pháp giải bài tập Bài 3.10 trang 74 SGK Toán 11 tập 1, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Một thấu kính hội tụ có tiêu cự f= 30 cm. Trong Vật lí, ta biết rằng nếu đặt vật thật AB cách quang tâm của thấu kính một khoảng d (cm) > 30 (cm) thì được ảnh thật A’B’ của thấu kính một khoảng d’ (cm) ( Hình 3.5).
Đề bài
Một thấu kính hội tụ có tiêu cự f= 30 cm. Trong Vật lí, ta biết rằng nếu đặt vật thật AB cách quang tâm của thấu kính một khoảng d (cm) > 30 (cm) thì được ảnh thật A’B’ của thấu kính một khoảng d’ (cm) ( Hình 3.5). Ngược lại, nếu 0<d<30, ta có ảnh ảo. Công thức của thấu kính là \(\frac{1}{d} + \frac{1}{{d'}} = \frac{1}{{30}}\)
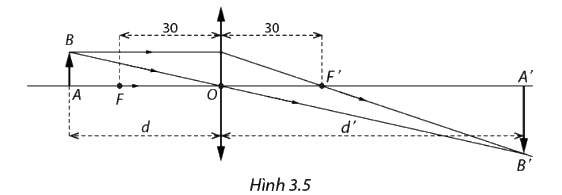
a, Từ công thức của thấu kính, hãy tìm biểu thức xác định hàm số d’= h (d)
b, Tìm các giới hạn \(\mathop {\lim }\limits_{x \to {{30}^ + }} h(d),\mathop {\lim }\limits_{x \to {{30}^ - }} h(d)\) và \(\mathop {\lim }\limits_{x \to + \infty } h(d)\). Sử dụng các kết quả này để giải thích ý nghĩa đã biết trong Vật lí.
Phương pháp giải - Xem chi tiết
a, Từ công thức rút d’ theo d.
b, Sử dụng giới hạn trái, giới hạn phải, giới hạn tại vô cực.
Lời giải chi tiết
a, Ta có : \(h(d) = \frac{1}{d} + \frac{1}{{d'}} = \frac{1}{{30}} \Rightarrow \frac{1}{{d'}} = \frac{1}{{30}} - \frac{1}{d} = \frac{{d - 30}}{{30d}} \Rightarrow d' = \frac{{30d}}{{d - 30}}\)
b, Ta có: \(\mathop {\lim }\limits_{d \to {{30}^ + }} 30d = 900\), \(\mathop {\lim }\limits_{d \to {{30}^ + }} (d - 30) = 0\) và d-30 > 0
\( \Rightarrow \mathop {\lim }\limits_{d \to {{30}^ + }} h(d) = \mathop {\lim }\limits_{d \to {{30}^ + }} \frac{{30d}}{{d - 30}} = + \infty \)
Ta có: \(\mathop {\lim }\limits_{d \to {{30}^ - }} 30d = 900\), \(\mathop {\lim }\limits_{d \to {{30}^ - }} (d - 30) = 0\) và d – 30 < 0
\( \Rightarrow \mathop {\lim }\limits_{d \to {{30}^ - }} h(d) = \mathop {\lim }\limits_{d \to {{30}^ - }} \frac{{30d}}{{d - 30}} = - \infty \)
Ta có: \(\mathop {\lim }\limits_{d \to + \infty } h(d) = \mathop {\lim }\limits_{d \to + \infty } \frac{{30d}}{{d - 30}} = \mathop {\lim }\limits_{d \to + \infty } \frac{{30}}{{1 - \frac{{30}}{d}}} = 30\).
Bài 3.10 trang 74 SGK Toán 11 tập 1 thuộc chương trình Đại số và Giải tích lớp 11, cụ thể là phần Vectơ trong mặt phẳng. Bài toán này thường yêu cầu học sinh áp dụng kiến thức về tích vô hướng của hai vectơ để chứng minh các đẳng thức vectơ, tính góc giữa hai vectơ, hoặc xác định điều kiện để hai vectơ vuông góc.
Thông thường, bài toán sẽ cho trước các vectơ và yêu cầu:
Để giải bài 3.10 trang 74 SGK Toán 11 tập 1 hiệu quả, học sinh cần nắm vững các kiến thức và công thức sau:
Bài toán: Cho hai vectơ a = (2; -1) và b = (1; 3). Tính tích vô hướng của a và b, và xác định góc giữa hai vectơ.
Giải:
Để củng cố kiến thức, học sinh có thể tự giải các bài tập tương tự trong SGK và sách bài tập Toán 11 tập 1. Ngoài ra, có rất nhiều bài tập trực tuyến và tài liệu tham khảo khác có sẵn trên internet.
Bài 3.10 trang 74 SGK Toán 11 tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán về vectơ. Bằng cách nắm vững kiến thức và phương pháp giải, học sinh có thể tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.
| Công thức | Mô tả |
|---|---|
| a.b = |a||b|cos(θ) | Tích vô hướng của hai vectơ |
| a.b = 0 | Điều kiện hai vectơ vuông góc |
| cos(θ) = (a.b) / (|a||b|) | Công thức tính cosin góc giữa hai vectơ |