Bài 4.37 thuộc chương trình Toán 11 tập 1, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh hiểu rõ các quy tắc tính đạo hàm và cách áp dụng chúng vào việc tìm cực trị của hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 4.37, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình hộp ABCD.A'B'C'D'. Gọi \(O = AC \cap BD\) và \(O' = A'C' \cap B'D'\). Gọi M, N lần lượt là trung điểm của AB và CD.
Đề bài
Cho hình hộp ABCD.A'B'C'D'. Gọi \(O = AC \cap BD\) và \(O' = A'C' \cap B'D'\). Gọi M, N lần lượt là trung điểm của AB và CD. Ảnh của tam giác C'MN qua phép chiếu song song trên mặt phẳng (ABCD) theo phương AO' là
A. Đoạn thẳng MN.
B. Tam giác OBC.
C. Tam giác CMN.
D. Đoạn thẳng BD.
Phương pháp giải - Xem chi tiết
A' là hình chiếu song song của điểm A trên (P) theo phương d thì AA' // d và AA' cắt (P) tại A'.
Lời giải chi tiết
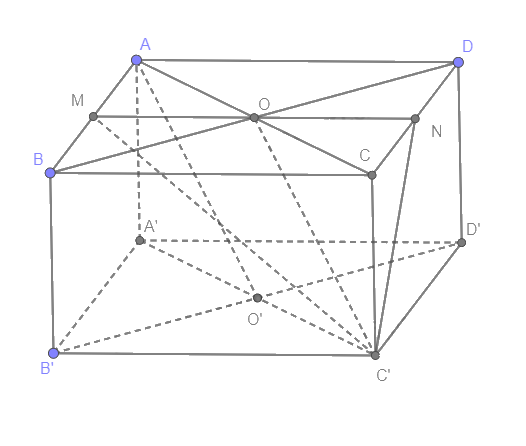
M, N thuộc (ABCD) nên M, N là hình chiếu song song của chính nó trên (ABCD) theo phương AO'
Ta có: AA' // CC' (cùng // BB') và AA' = CC' (cùng = CC') nên ACC'A' là hình bình hành. Suy ra AC // A'C' hay AO // O'C' (1)
O, O' lần lượt là giao điểm các đường chéo của hình bình ABCD, A'B'C'D' nên O là trung điểm AC, A'C'. Suy ra AO = O'C' (2)
Từ (1), (2) suy ra AOC'O' là hình bình hành. Suy ra AO' // OC'
Vậy O là hình chiếu song song của C' trên (ABCD) theo phương AO'
Suy ra hình chiếu song song của tam giác C'MN trên (ABCD) theo phương AO' là đoạn thẳng MN.
Chọn đáo án A.
Bài 4.37 trang 125 SGK Toán 11 tập 1 là một bài tập quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững kiến thức về đạo hàm và ứng dụng của nó trong việc tìm cực trị của hàm số. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Đề bài yêu cầu chúng ta tìm cực trị của hàm số. Để làm được điều này, chúng ta cần thực hiện các bước sau:
Giả sử hàm số cần xét là f(x) = ax3 + bx2 + cx + d (với a, b, c, d là các hằng số). (Đây chỉ là một ví dụ minh họa, đề bài cụ thể sẽ có hàm số khác).
Bước 1: Tính đạo hàm bậc nhất:
f'(x) = 3ax2 + 2bx + c
Bước 2: Tìm các điểm làm đạo hàm bậc nhất bằng 0:
Giải phương trình 3ax2 + 2bx + c = 0. Phương trình này có thể có hai nghiệm phân biệt (x1, x2), một nghiệm kép hoặc không có nghiệm.
Bước 3: Khảo sát dấu của đạo hàm bậc nhất:
Xét dấu của f'(x) trên các khoảng (-∞, x1), (x1, x2) và (x2, +∞). Nếu f'(x) đổi dấu từ dương sang âm tại x1 thì x1 là điểm cực đại. Nếu f'(x) đổi dấu từ âm sang dương tại x2 thì x2 là điểm cực tiểu.
Bước 4: Tính đạo hàm bậc hai:
f''(x) = 6ax + 2b
Bước 5: Kết luận:
Nếu f''(x1) < 0 thì x1 là điểm cực đại. Nếu f''(x2) > 0 thì x2 là điểm cực tiểu.
Xét hàm số f(x) = x3 - 3x2 + 2.
f'(x) = 3x2 - 6x
Giải phương trình 3x2 - 6x = 0, ta được x = 0 và x = 2.
f''(x) = 6x - 6
f''(0) = -6 < 0, vậy x = 0 là điểm cực đại và f(0) = 2.
f''(2) = 6 > 0, vậy x = 2 là điểm cực tiểu và f(2) = -2.
Để củng cố kiến thức, bạn có thể giải các bài tập tương tự trong SGK Toán 11 tập 1 hoặc trên các trang web học toán online khác. Việc luyện tập thường xuyên sẽ giúp bạn nắm vững kiến thức và tự tin giải các bài tập khó hơn.
Hy vọng lời giải chi tiết và hướng dẫn này sẽ giúp bạn hiểu rõ hơn về Bài 4.37 trang 125 SGK Toán 11 tập 1. Chúc bạn học tốt!