Chào mừng các em học sinh đến với bài giải chi tiết mục 1 trang 2 SGK Toán 11 tập 1 trên giaitoan.edu.vn. Bài viết này sẽ cung cấp cho các em lời giải đầy đủ, dễ hiểu, giúp các em hiểu rõ hơn về kiến thức và phương pháp giải bài tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng cao, hỗ trợ các em trong quá trình học tập môn Toán.
Trong mỗi Hình 1.1a, 1.1b, 1.1c và 1.1d, điểm M di động trên đường tròn tâm O từ A đến B theo chiều mũi tên.
Trong mỗi Hình 1.1a, 1.1b, 1.1c và 1.1d, điểm M di động trên đường tròn tâm O từ A đến B theo chiều mũi tên.
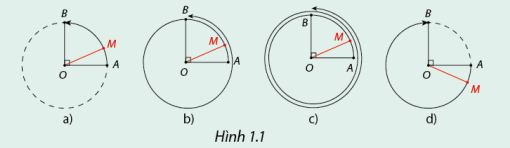
a) Với mỗi Hình 1.1a, 1.1b, 1.1c và 1.1d, cho biết điểm M di động trên đường tròn từ A đến B theo chiều quay của kim đồng hồ hay ngược với chiều quay của kim đồng hồ?
b) Số vòng quay khi điểm M di động trên đường tròn từ A đến B theo Hình 1.1b và theo Hình 1.1c lần lượt nhiều hơn bao nhiêu vòng so với số vòng quay khi điểm M di động trên đường tròn từ A đến B theo Hình 1.1a?
Phương pháp giải:
Quan sát hình vẽ để trả lời câu hỏi
Lời giải chi tiết:
a) Hình 1.1a, 1.1b, 1.1c: Điểm M di động trên đường tròn từ A đến B ngược chiều quay của kim đồng hồ.
Hình 1.1d: Điểm M di động trên đường tròn từ A đến B theo chiều quay của kim đồng hồ.
b) Số vòng quay ở Hình 1.1b nhiều hơn Hình 1.1a là 1 vòng.
Số vòng quay ở Hình 1.1c nhiều hơn Hình 1.1a là 2 vòng.
Mục 1 trang 2 SGK Toán 11 tập 1 thường xoay quanh các khái niệm cơ bản về hàm số, bao gồm định nghĩa hàm số, tập xác định, tập giá trị, và các tính chất của hàm số. Việc nắm vững những khái niệm này là nền tảng quan trọng để học tốt các phần kiến thức tiếp theo trong chương trình Toán 11.
Hàm số là một quy tắc tương ứng giữa mỗi phần tử của tập hợp A (tập xác định) với duy nhất một phần tử của tập hợp B (tập giá trị). Ký hiệu: y = f(x), trong đó x thuộc A, y thuộc B.
Tập xác định của hàm số là tập hợp tất cả các giá trị của x sao cho hàm số f(x) có nghĩa. Để tìm tập xác định, ta cần xác định các điều kiện để hàm số có nghĩa, ví dụ như mẫu số khác 0, căn thức có nghĩa, logarit có cơ số khác 1 và lớn hơn 0, v.v.
Tập giá trị của hàm số là tập hợp tất cả các giá trị của y mà hàm số f(x) có thể nhận được. Việc tìm tập giá trị thường khó khăn hơn so với tìm tập xác định và đòi hỏi phải phân tích kỹ lưỡng tính chất của hàm số.
Bài tập 1: Tìm tập xác định của hàm số y = √(2x - 1).
Hướng dẫn giải: Hàm số có nghĩa khi và chỉ khi 2x - 1 ≥ 0, tức là x ≥ 1/2. Vậy tập xác định của hàm số là [1/2, +∞).
Bài tập 2: Xét tính chẵn lẻ của hàm số y = x2 + 1.
Hướng dẫn giải: Ta có f(-x) = (-x)2 + 1 = x2 + 1 = f(x). Vậy hàm số là hàm số chẵn.
Kiến thức về hàm số có ứng dụng rộng rãi trong nhiều lĩnh vực của toán học và khoa học kỹ thuật. Ví dụ, trong vật lý, hàm số được sử dụng để mô tả mối quan hệ giữa các đại lượng vật lý như vận tốc, gia tốc, và thời gian. Trong kinh tế, hàm số được sử dụng để mô tả mối quan hệ giữa cung và cầu, chi phí và doanh thu.
| Công thức | Mô tả |
|---|---|
| y = f(x) | Định nghĩa hàm số |
| f(-x) = f(x) | Hàm số chẵn |
| f(-x) = -f(x) | Hàm số lẻ |
Hy vọng bài giải chi tiết này sẽ giúp các em hiểu rõ hơn về mục 1 trang 2 SGK Toán 11 tập 1. Chúc các em học tập tốt!