Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 1 của giaitoan.edu.vn. Ở đây, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Toán 11 tập 1, đặc biệt là mục 1 trang 8, 9, 10, 11.
Mục tiêu của chúng tôi là giúp các em học toán hiệu quả hơn, nắm vững kiến thức và tự tin giải quyết các bài toán khó.
Trên đường tròn lượng giác, gọi M và N lần lượt là điểm biểu diễn của góc lượng giác có số đo \(\frac{{9\pi }}{4}\) và \( - \frac{\pi }{6}\). Tìm tọa độ của M và N.
Trên đường tròn lượng giác, gọi M và N lần lượt là điểm biểu diễn của góc lượng giác có số đo \(\frac{{9\pi }}{4}\) và \( - \frac{\pi }{6}\). Tìm tọa độ của M và N.
Phương pháp giải:
Áp dụng công thức lượng giác:
Lời giải chi tiết:
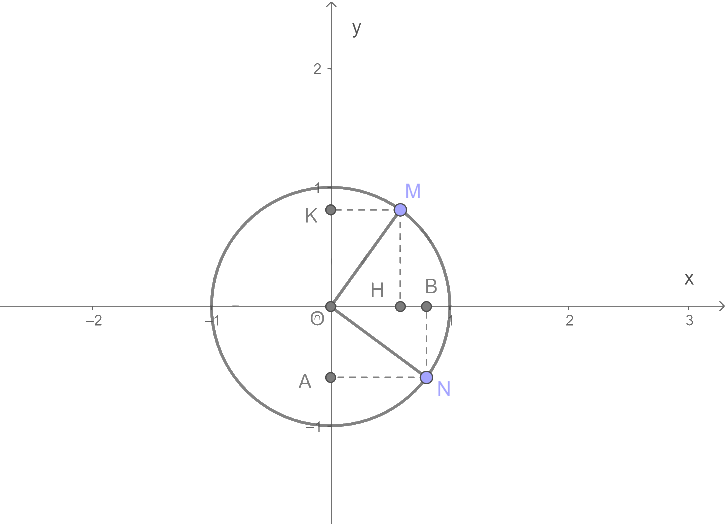
Gọi các điểm như trên hình vẽ
Gọi x và y lần lượt là hoành độ và tung độ của M \(\left( {x > 0,y > 0} \right)\)
Vì tam giác OMH vuông tại H và có góc \(\widehat {MOH} = \frac{\pi }{4}\) nên \(OH = OM.\cos \frac{\pi }{4} = \frac{{\sqrt 2 }}{2}\)
Vì tam giác OKM vuông tại K và có góc \(\widehat {MOK} = \frac{\pi }{4}\) nên \(OK = OM.\cos \frac{\pi }{4} = \frac{{\sqrt 2 }}{2}\).
Mà \(x > 0,y > 0\) nên \(M\left( {\frac{{\sqrt 2 }}{2};\frac{{\sqrt 2 }}{2}} \right)\)
Gọi z và t là hoành độ và tung độ của N \(\left( {z > 0,t < 0} \right)\)
Vì tam giác OBN vuông tại B có góc \(\widehat {BON} = \frac{\pi }{6}\) nên \(OB = ON.\cos \frac{\pi }{6} = \frac{{\sqrt 3 }}{2}\)
Vì tam giác OAN vuông tại A có góc \(\widehat {AON} = \frac{\pi }{3}\) nên \(OA = ON.\cos \frac{\pi }{3} = \frac{1}{2}\)
Mà \(z > 0,t < 0\) nên \(N\left( {\frac{{\sqrt 3 }}{2}; - \frac{1}{2}} \right)\).
Tìm các giá trị lượng giác của góc 3300.
Phương pháp giải:
Áp dụng công thức lượng giác:

Lời giải chi tiết:

Trên đường tròn lượng giác, gọi M là điểm biểu diễn của góc lượng giác 3300
Gọi x và y lần lượt là hoành độ và tung độ của M. Ta có: \(x > 0,y < 0\)
Vì tam giác OMH vuông tại H và có góc \(\widehat {MOH} = {30^0}\) nên \(OH = OM.\cos {30^0} = \frac{{\sqrt 3 }}{2}\)
Vì tam giác OKM vuông tại K và có góc \(\widehat {MOK} = {60^0}\) nên \(OK = OM.\cos {60^0} = \frac{1}{2}\)
Suy ra: \(\cos {330^0} = x = \frac{{\sqrt 3 }}{2}\), \(\sin {330^0} = y = - \frac{1}{2}\)
\( \Rightarrow \tan {330^0} = \frac{{\sin {{330}^0}}}{{\cos {{330}^0}}} = \left( { - \frac{1}{2}} \right):\frac{{\sqrt 3 }}{2} = - \frac{{\sqrt 3 }}{3}\)
\( \Rightarrow \cot {330^0} = \frac{{\cos {{330}^0}}}{{\sin {{330}^0}}} = \frac{{\sqrt 3 }}{2}:\left( { - \frac{1}{2}} \right) = - \sqrt 3 \)
Hãy viết lại bảng các giá trị lượng giác của một số góc đặc biệt từ 00 đến 900 đã học ở lớp 10.
Phương pháp giải:
Xem lại sách lớp 10
Lời giải chi tiết:

Tính \(\sin \left( { - \frac{{35\pi }}{6}} \right),\cos \left( { - \frac{{35\pi }}{6}} \right),\tan \left( { - \frac{{35\pi }}{6}} \right),\cot \left( { - \frac{{35\pi }}{6}} \right)\).
Phương pháp giải:
\(\begin{array}{l}\sin \left( {\alpha + k2\pi } \right) = \sin \alpha \\\cos \left( {\alpha + k2\pi } \right) = \cos \alpha \\\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\\\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}\end{array}\)
Lời giải chi tiết:
\(\begin{array}{l}\sin \left( { - \frac{{35\pi }}{6}} \right) = \sin \left( { - 6\pi + \frac{\pi }{6}} \right) = \sin \left( {\frac{\pi }{6}} \right) = \frac{1}{2}\\\cos \left( { - \frac{{35\pi }}{6}} \right) = \cos \left( { - 6\pi + \frac{\pi }{6}} \right) = \cos \left( {\frac{\pi }{6}} \right) = \frac{{\sqrt 3 }}{2}\\\tan \left( { - \frac{{35\pi }}{6}} \right) = \frac{{\sin \left( { - \frac{{35\pi }}{6}} \right)}}{{\cos \left( { - \frac{{35\pi }}{6}} \right)}} = \frac{{\sqrt 3 }}{3}\\\cot \left( { - \frac{{35\pi }}{6}} \right) = \frac{{\cos \left( { - \frac{{35\pi }}{6}} \right)}}{{\sin \left( { - \frac{{35\pi }}{6}} \right)}} = \sqrt 3 \end{array}\)
Tính \(\sin {315^0},\cos \frac{{12\pi }}{7},\tan \left( { - {{168}^0}} \right)\).
Phương pháp giải:
Sử dụng máy tính cầm tay.
Lời giải chi tiết:
\(\sin \left( {{{315}^0}} \right) = - \frac{{\sqrt 2 }}{2}\)
\(\cos \frac{{12\pi }}{7} \approx 0,62\)
\(\tan \left( { - {{168}^0}} \right) \approx 0,21\)
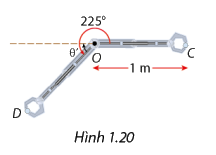
Một cánh tay robot dài 1m được điều khiển để gắp một vật tại điểm C, rồi xoay theo chiều dương một góc 2250 để thả vật tại điểm D như Hình 1.20. Chọn hệ trục tọa độ Oxy sao cho tâm của cánh tay robot trùng với O và C có tọa độ là (1; 0). Tìm tọa độ của vật tại điểm D.

Phương pháp giải:
Hoành độ của điểm D là \(\cos {225^0}\), tung độ của điểm D là \(\sin {225^0}\).
Lời giải chi tiết:

Gọi x và y là hoành độ và tung độ của D
\(\begin{array}{l}x = \cos {225^0} = - \frac{{\sqrt 2 }}{2}\\y = \sin {225^0} = - \frac{{\sqrt 2 }}{2}\end{array}\)
Vậy \(D\left( { - \frac{{\sqrt 2 }}{2}; - \frac{{\sqrt 2 }}{2}} \right)\).
Mục 1 của SGK Toán 11 tập 1 thường tập trung vào các kiến thức cơ bản về dãy số, giới hạn dãy số và các ứng dụng của chúng. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập trong mục 1, trang 8, 9, 10, 11, đồng thời phân tích phương pháp giải và các lưu ý quan trọng.
Bài 1 thường yêu cầu học sinh vận dụng kiến thức về dãy số để xác định số hạng tổng quát, tính tổng của dãy số hoặc chứng minh một tính chất nào đó của dãy số. Để giải bài tập này, các em cần nắm vững các công thức và định lý liên quan đến dãy số, đồng thời rèn luyện kỹ năng biến đổi đại số.
Bài 2 thường liên quan đến giới hạn của dãy số. Để giải bài tập này, các em cần hiểu rõ khái niệm giới hạn, các tính chất của giới hạn và các phương pháp tính giới hạn. Một số phương pháp thường được sử dụng bao gồm phương pháp chia, phương pháp đặt ẩn phụ và phương pháp sử dụng định lý giới hạn.
Bài 3 có thể yêu cầu học sinh áp dụng kiến thức về dãy số và giới hạn dãy số để giải quyết các bài toán thực tế. Ví dụ, bài toán về tính lãi kép, bài toán về sự tăng trưởng dân số hoặc bài toán về sự phân rã phóng xạ. Để giải bài tập này, các em cần phân tích đề bài, xác định các yếu tố liên quan và xây dựng mô hình toán học phù hợp.
Bài 4 thường là bài tập tổng hợp, yêu cầu học sinh vận dụng kiến thức của cả mục 1 để giải quyết. Để giải bài tập này, các em cần nắm vững các khái niệm, công thức và phương pháp giải đã học, đồng thời rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
| Công thức | Mô tả |
|---|---|
| Số hạng tổng quát của dãy số cộng: | un = u1 + (n-1)d |
| Tổng của n số hạng đầu tiên của dãy số cộng: | Sn = n(u1 + un)/2 |
| Số hạng tổng quát của dãy số nhân: | un = u1qn-1 |
| Tổng của n số hạng đầu tiên của dãy số nhân: | Sn = u1(1-qn)/(1-q) |
Hy vọng với những lời giải chi tiết và phương pháp giải bài tập được trình bày trong bài viết này, các em sẽ học tốt môn Toán 11 tập 1 và đạt kết quả cao trong các kỳ thi. Chúc các em thành công!