Bài 8.39 trang 89 SGK Toán 11 tập 2 là một bài tập quan trọng trong chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng giải bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài tập này đòi hỏi học sinh phải nắm vững các kiến thức cơ bản về đạo hàm, cực trị và điểm uốn của hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 8.39 trang 89 SGK Toán 11 tập 2, giúp các em học sinh hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Cho hình lập phương ABCD.A’B’C’D’ cạnh a.
Đề bài
Cho hình lập phương ABCD.A’B’C’D’ cạnh a.
a) Chứng minh BC vuông góc với mặt phẳng (A’B’CD).
b) Tính khoảng cách giữa hai đường thẳng AB’ và BC’.
Phương pháp giải - Xem chi tiết
Đường thẳng d vuông góc với 2 đường thẳng cắt nhau nằm trong (P) thì d vuông góc với (P).
Lời giải chi tiết
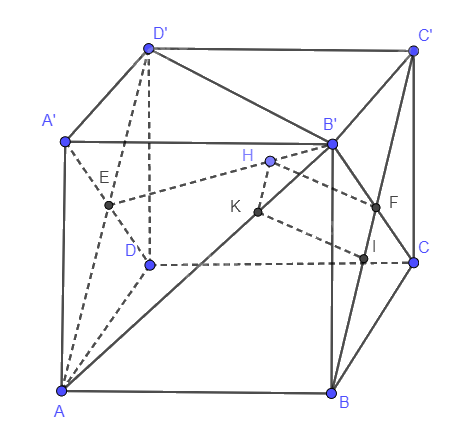
a) BC vuông góc với CD (ABCD là hình vuông)
BC vuông với (ADD’A’) nên BC vuông góc với A’D
Suy ra BC vuông góc với (A’B’CD)
b) Gọi giao điểm của B’C và BC’ là F, A’D và AD’ là E
Kẻ FH vuông góc với BC’ nên FH vuông góc với AD’
Kẻ HK // BC’, KI // HF
Vậy KI là đường vuông góc chung của AB’ và BC’.
Bài 8.39 trang 89 SGK Toán 11 tập 2 yêu cầu học sinh giải một bài toán liên quan đến việc khảo sát hàm số bậc ba bằng phương pháp đạo hàm. Để giải bài toán này một cách hiệu quả, chúng ta cần thực hiện các bước sau:
Giả sử hàm số cần khảo sát là: y = x3 - 3x2 + 2
Bước 1: Tính đạo hàm bậc nhất
y' = 3x2 - 6x
Bước 2: Tìm điểm cực trị
Giải phương trình y' = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy x = 0 hoặc x = 2
Bước 3: Tính đạo hàm bậc hai
y'' = 6x - 6
Bước 4: Xác định tính chất của điểm cực trị
Bước 5: Tìm điểm uốn
Giải phương trình y'' = 0:
6x - 6 = 0
x = 1
Vậy hàm số có điểm uốn tại x = 1. Giá trị tại điểm uốn là y(1) = 0.
Bước 6: Lập bảng biến thiên
| x | -∞ | 0 | 1 | 2 | +∞ |
|---|---|---|---|---|---|
| y' | + | 0 | - | 0 | + |
| y | ↗ | 2 (CĐ) | ↘ | 0 (DI) | ↗ |
Bước 7: Vẽ đồ thị hàm số
Dựa vào bảng biến thiên, ta có thể vẽ được đồ thị hàm số y = x3 - 3x2 + 2.
Hy vọng với hướng dẫn chi tiết này, các em học sinh có thể tự tin giải Bài 8.39 trang 89 SGK Toán 11 tập 2 và các bài tập tương tự. Hãy luyện tập thường xuyên để nắm vững kiến thức và kỹ năng giải toán.