Bài 6.13 trang 19 SGK Toán 11 tập 2 là một bài tập quan trọng trong chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng giải bài toán liên quan đến đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để tìm đạo hàm của hàm số và giải các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu và phương pháp giải nhanh chóng cho Bài 6.13 trang 19 SGK Toán 11 tập 2, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
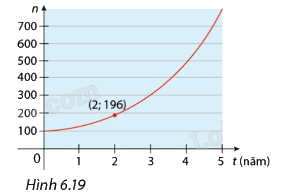
Lúc đầu trong ao có một số con ếch. Người ta ghi nhận số lượng ếch trong 5 năm đầu như Hình 6.19. Giả sử số lượng ếch tăng theo hàm số \(n\left( t \right) = C.{a^t}\).
Đề bài
Lúc đầu trong ao có một số con ếch. Người ta ghi nhận số lượng ếch trong 5 năm đầu như Hình 6.19. Giả sử số lượng ếch tăng theo hàm số \(n\left( t \right) = C.{a^t}\).
a) Tính số lượng ếch lúc ban đầu.
b) Tìm hàm số biểu diễn số lượng ếch sau t năm kể từ khi chúng xuất hiện trong ao.
c) Dự đoán số lượng ếch sau 15 năm.
Phương pháp giải - Xem chi tiết
a) Số lượng ếch ban đầu là n khi t = 0.
b) Dựa vào các điểm thuộc đồ thị để tìm C, a.
Số lượng ếch mỗi năm bằng số lượng ếch ban đầu cộng với số lượng ếch tăng theo hàm số \(n\left( t \right) = C.{a^t}\).
c) Thay t = 15 vào hàm số tìm được ở phần b.
Lời giải chi tiết
a) Số lượng ếch ban đầu là 100 con.
b) Đồ thị hàm số đi qua 2 điểm (0; 100) và (2; 196). Ta có:
\(\left\{ \begin{array}{l}C.{a^0} = 100\\C.{a^2} = 196\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}C = 100\\{a^2} = 1,96\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}C = 100\\a = 1,4\end{array} \right.\)
\( \Rightarrow n\left( t \right) = 100.1,{4^t}\)
Vậy hàm số biểu diễn số lượng ếch sau t năm kể từ khi chúng xuất hiện trong ao là:
\(H\left( t \right) = 100 + 100.1,{4^t}\)
c) \(H\left( {15} \right) = 100 + 100.1,{4^{15}} \approx 15656\) (con).
Bài 6.13 trang 19 SGK Toán 11 tập 2 thuộc chương trình học về đạo hàm của hàm số. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
Nội dung bài tập: Bài 6.13 thường yêu cầu học sinh tính đạo hàm của một hàm số cho trước hoặc giải một phương trình, bất phương trình liên quan đến đạo hàm. Để giải bài tập này, học sinh cần thực hiện các bước sau:
Ví dụ minh họa:
Giả sử bài tập yêu cầu tính đạo hàm của hàm số f(x) = x2 + 2x + 1. Ta có:
f'(x) = 2x + 2
Vậy, đạo hàm của hàm số f(x) là f'(x) = 2x + 2.
Lưu ý khi giải bài tập:
Mở rộng kiến thức:
Ngoài việc giải Bài 6.13 trang 19 SGK Toán 11 tập 2, học sinh nên tìm hiểu thêm về các ứng dụng của đạo hàm trong thực tế, chẳng hạn như việc tìm cực trị của hàm số, vẽ đồ thị hàm số, giải các bài toán tối ưu hóa. Việc mở rộng kiến thức sẽ giúp học sinh hiểu sâu hơn về đạo hàm và ứng dụng của nó trong các lĩnh vực khác.
Tài liệu tham khảo:
Kết luận:
Bài 6.13 trang 19 SGK Toán 11 tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán liên quan đến đạo hàm. Bằng cách nắm vững kiến thức cơ bản, áp dụng các quy tắc tính đạo hàm một cách chính xác và luyện tập thường xuyên, học sinh có thể tự tin giải bài tập này và các bài tập tương tự. Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán.