Chào mừng bạn đến với bài học về Lý thuyết Hàm số liên tục, một phần quan trọng trong chương trình SGK Toán 11. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và nâng cao về hàm số liên tục, giúp bạn hiểu rõ hơn về tính liên tục của hàm số và ứng dụng của nó trong giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cam kết mang đến cho bạn những bài giảng chất lượng, dễ hiểu và bài tập đa dạng để bạn có thể tự tin chinh phục môn Toán.
I. Hàm số liên tục tại một điểm và liên tục trên một khoảng
I. Hàm số liên tục tại một điểm và liên tục trên một khoảng
1. Hàm số liên tục tại 1 điểm
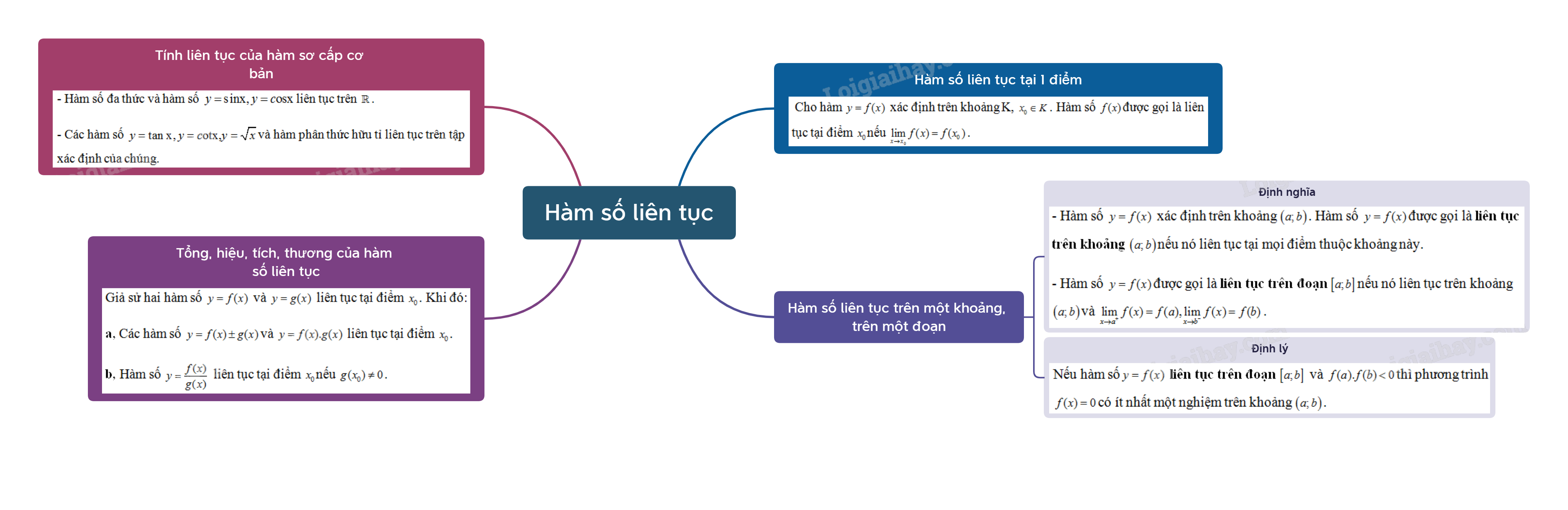
Cho hàm \(y = f(x)\) xác định trên khoảng K, \({x_0} \in K\). Hàm số \(f(x)\) được gọi là liên tục tại điểm \({x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = f({x_0})\).
Hàm số không liên tục tại \({x_0}\) được gọi là gián đoạn tại điểm đó.
2. Hàm số liên tục trên một khoảng
- Hàm số \(y = f(x)\) xác định trên khoảng \(\left( {a;b} \right)\)
Hàm số \(y = f(x)\) được gọi là liên tục trên khoảng \(\left( {a;b} \right)\) nếu nó liên tục tại mọi điểm thuộc khoảng này.
- Hàm số \(y = f(x)\) được gọi là liên tục trên đoạn \(\left[ {a;b} \right]\) nếu nó liên tục trên khoảng \(\left( {a;b} \right)\) và \(\mathop {\lim }\limits_{x \to {a^ + }} f(x) = f(a),\mathop {\lim }\limits_{x \to {b^ - }} f(x) = f(b)\).
* Nhận xét:
- Đồ thị hàm số liên tục trên một khoảng, đoạn là “đường liền” trên khoảng, đoạn đó.
- Nếu hàm số\(y = f(x)\) liên tục trên đoạn \(\left[ {a;b} \right]\) và \(f(a).f(b) < 0\)thì phương trình \(f(x) = 0\)có ít nhất một nghiệm trên khoảng \(\left( {a;b} \right)\).
II. Một số định lí cơ bản
1. Định lí 1
- Hàm số đa thức và hàm số \(y = {\mathop{\rm s}\nolimits} {\rm{inx}},y = c{\rm{osx}}\)liên tục trên \(\mathbb{R}\).
- Các hàm số \(y = \tan {\rm{x}},y = c{\rm{otx,}}y = \sqrt x \) và hàm phân thức hữu tỉ (thương của hai đa thức) liên tục trên tập xác định của chúng.
2. Định lí 2
Giả sử hai hàm số \(y = f(x)\) và \(y = g(x)\) liên tục tại điểm \({x_0}\). Khi đó:
a, Các hàm số \(y = f(x) \pm g(x)\) và \(y = f(x).g(x)\) liên tục tại điểm \({x_0}\).
b, Hàm số \(y = \frac{{f(x)}}{{g(x)}}\) liên tục tại điểm \({x_0}\) nếu \(g({x_0}) \ne 0\).
c, Hàm số \(y = f(x)\) liên tục trên khoảng K và \(f(x) \ge 0,\forall x \in K\). Khi đó hàm số \(y = \sqrt {f(x)} \) liên tục trên K.
Hàm số liên tục là một khái niệm cơ bản và quan trọng trong giải tích. Nó mô tả tính chất của một hàm số khi giá trị đầu vào thay đổi liên tục. Hiểu rõ về hàm số liên tục là nền tảng để học các khái niệm nâng cao hơn như đạo hàm, tích phân và ứng dụng của chúng trong các lĩnh vực khoa học và kỹ thuật.
Một hàm số f(x) được gọi là liên tục tại điểm x0 nếu thỏa mãn ba điều kiện sau:
Một hàm số f(x) được gọi là liên tục trên khoảng (a, b) nếu nó liên tục tại mọi điểm trong khoảng đó.
Hàm số liên tục có nhiều ứng dụng trong các lĩnh vực khác nhau, bao gồm:
Ví dụ 1: Xét hàm số f(x) = x2 + 1. Hàm số này là hàm đa thức, do đó nó liên tục trên tập số thực.
Ví dụ 2: Xét hàm số f(x) = 1/x. Hàm số này là hàm hữu tỉ, nó liên tục trên tập xác định của nó là x ≠ 0.
Hy vọng bài học này đã cung cấp cho bạn những kiến thức hữu ích về Lý thuyết Hàm số liên tục - SGK Toán 11. Chúc bạn học tập tốt!