Lý thuyết Hàm số lượng giác và đồ thị - SGK Toán 11

Lý thuyết Hàm số lượng giác và đồ thị - SGK Toán 11 Cùng khám phá

Lý thuyết Hàm số lượng giác và đồ thị - SGK Toán 11

Chào mừng bạn đến với chuyên mục Lý thuyết Hàm số lượng giác và đồ thị của chương trình Toán 11. Tại giaitoan.edu.vn, chúng tôi cung cấp kiến thức nền tảng vững chắc, giúp bạn hiểu rõ các khái niệm, tính chất và ứng dụng của hàm số lượng giác.

Học cùng chúng tôi, bạn sẽ được tiếp cận với phương pháp giảng dạy dễ hiểu, bài tập đa dạng và các ví dụ minh họa sinh động.

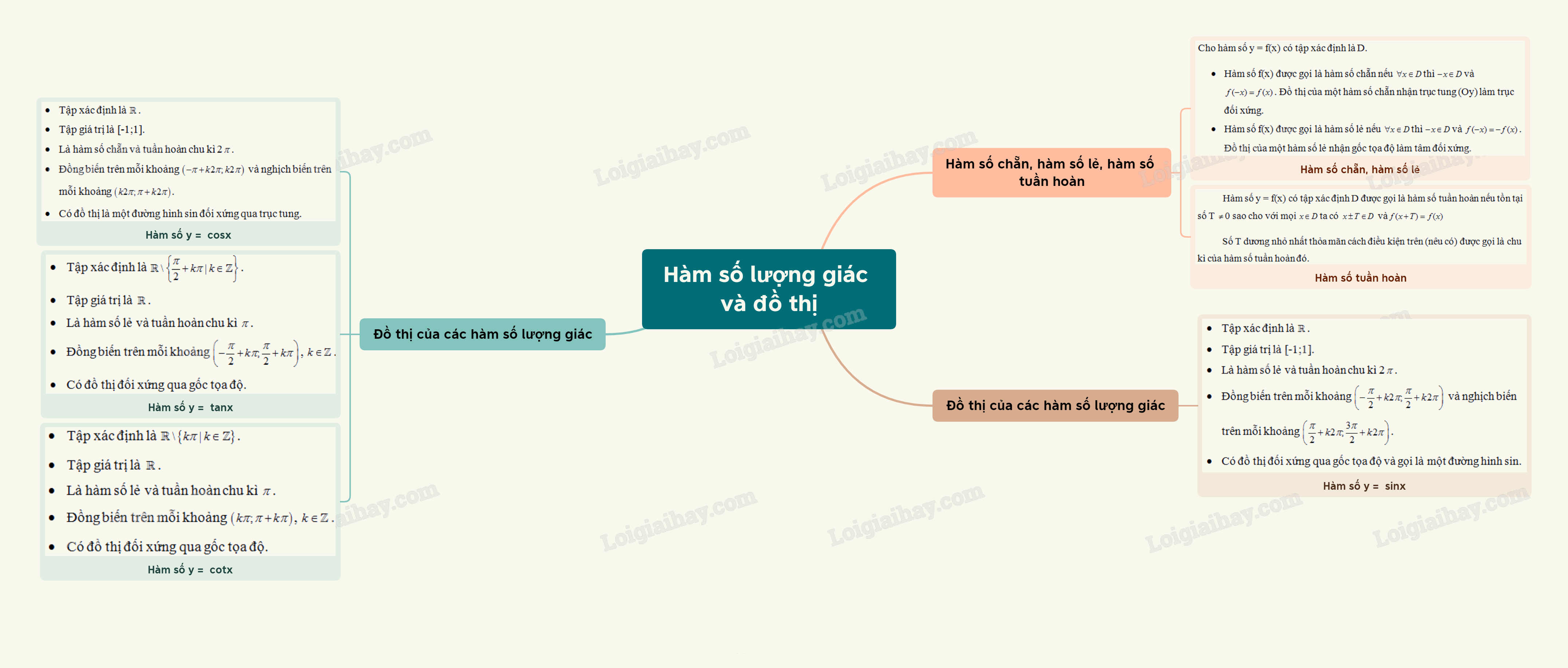
I. Hàm số chẵn, hàm số lẻ, hàm số tuần hoàn

1. Hàm số chẵn, hàm số lẻ

Cho hàm số y = f(x) có tập xác định là D.

Hàm số f(x) được gọi là hàm số chẵn nếu \(\forall x \in D\) thì \( - x \in D\) và \(f( - x) = f(x)\)

Hàm số f(x) được gọi là hàm số lẻ nếu \(\forall x \in D\) thì \( - x \in D\) và \(f( - x) = - f(x)\)

* Lưu ý:

Đồ thị của một hàm số chẵn nhận trục tung (Oy) làm trục đối xứng.
Đồ thị của một hàm số lẻ nhận gốc tọa độ làm tâm đối xứng.

2. Hàm số tuần hoàn

Hàm số y = f(x) có tập xác định D được gọi là hàm số tuần hoàn nếu tồn tại số T \( \ne \) 0 sao cho với mọi \(x \in D\) ta có \(x \pm T \in D\) và \(f(x + T) = f(x)\)

Số T dương nhỏ nhất thỏa mãn cách điều kiện trên (nêu có) được gọi là chu kì của hàm số tuần hoàn đó.

* Nhận xét:

Các hàm số y = sinx, y=cosx tuần hoàn chu kì 2\(\pi \).

Các hàm số y = tanx, y=cotx tuần hoàn chu kì \(\pi \).

II. Hàm số lượng giác

1. Định nghĩa các hàm số lượng giác

Quy tắc đặt tương ứng mỗi số thực x với số thực sinx được gọi là hàm số sin, kí hiệu y = sinx. Tập xác định của hàm số sin là \(\mathbb{R}\).
Quy tắc đặt tương ứng mỗi số thực x với số thực cosx được gọi là hàm số cos, kí hiệu y = cosx. Tập xác định của hàm số côsin là \(\mathbb{R}\).
Hàm số cho bằng công thức \(y = \frac{{\sin \alpha }}{{\cos \alpha }}\)được gọi là hàm số tang, kí hiệu là y = tanx. Tập xác định của hàm số tang là \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\).
Hàm số cho bằng công thức \(y = \frac{{\cos \alpha }}{{\sin \alpha }}\)được gọi là hàm số côtang, kí hiệu là y = cotx. Tập xác định của hàm số côtang là \(\mathbb{R}\backslash \left\{ {k\pi |k \in \mathbb{Z}} \right\}\).

2. Đồ thị của các hàm số lượng giác

a, Hàm số y = sinx

Tập xác định là \(\mathbb{R}\).
Tập giá trị là [-1;1].
Là hàm số lẻ và tuần hoàn chu kì 2\(\pi \).
Đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\) và nghịch biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)\).
Có đồ thị đối xứng qua gốc tọa độ và gọi là một đường hình sin.

b, Hàm số y = cosx

Tập xác định là \(\mathbb{R}\).
Tập giá trị là [-1;1].
Là hàm số chẵn và tuần hoàn chu kì 2\(\pi \).
Đồng biến trên mỗi khoảng \(\left( { - \pi + k2\pi ;k2\pi } \right)\) và nghịch biến trên mỗi khoảng \(\left( {k2\pi ;\pi + k2\pi } \right)\).
Có đồ thị là một đường hình sin đối xứng qua trục tung.

c, Hàm số y = tanx

Tập xác định là \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\).
Tập giá trị là \(\mathbb{R}\).
Là hàm số lẻ và tuần hoàn chu kì \(\pi \).
Đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k\pi ;\frac{\pi }{2} + k\pi } \right)\), \(k \in \mathbb{Z}\).
Có đồ thị đối xứng qua gốc tọa độ.

d, Hàm số y = cotx

Tập xác định là \(\mathbb{R}\backslash \left\{ {k\pi |k \in \mathbb{Z}} \right\}\).
Tập giá trị là \(\mathbb{R}\).
Là hàm số lẻ và tuần hoàn chu kì \(\pi \).
Đồng biến trên mỗi khoảng \(\left( {k\pi ;\pi + k\pi } \right)\), \(k \in \mathbb{Z}\).
Có đồ thị đối xứng qua gốc tọa độ.

Lý thuyết Hàm số lượng giác và đồ thị - SGK Toán 11 Cùng khám phá 1

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Lý thuyết Hàm số lượng giác và đồ thị - SGK Toán 11 Cùng khám phá – hành trang không thể thiếu trong chuyên mục toán 11 trên nền tảng tài liệu toán. Bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Lý thuyết Hàm số lượng giác và đồ thị - SGK Toán 11

Hàm số lượng giác đóng vai trò quan trọng trong chương trình Toán học, đặc biệt là ở lớp 11. Việc nắm vững lý thuyết và kỹ năng vẽ đồ thị hàm số lượng giác là nền tảng để giải quyết các bài toán phức tạp hơn trong các chương trình học nâng cao và ứng dụng thực tế.

I. Các hàm số lượng giác cơ bản

Các hàm số lượng giác cơ bản bao gồm:

Hàm số sin (y = sin x): Định nghĩa, tập xác định, tập giá trị, tính tuần hoàn, tính chẵn lẻ, đồ thị.
Hàm số cosin (y = cos x): Định nghĩa, tập xác định, tập giá trị, tính tuần hoàn, tính chẵn lẻ, đồ thị.
Hàm số tang (y = tan x): Định nghĩa, tập xác định, tập giá trị, tính tuần hoàn, tính chẵn lẻ, đồ thị.
Hàm số cotang (y = cot x): Định nghĩa, tập xác định, tập giá trị, tính tuần hoàn, tính chẵn lẻ, đồ thị.

II. Đồ thị hàm số lượng giác

Đồ thị hàm số lượng giác là biểu diễn hình học của hàm số trên mặt phẳng tọa độ. Việc vẽ và phân tích đồ thị hàm số lượng giác giúp chúng ta hiểu rõ hơn về tính chất của hàm số, tìm ra các điểm đặc biệt như điểm cực trị, điểm đối xứng và các khoảng đồng biến, nghịch biến.

1. Đồ thị hàm số y = sin x:

Tập xác định: R
Tập giá trị: [-1; 1]
Tính tuần hoàn: T = 2π
Tính chẵn lẻ: Hàm số lẻ

Đồ thị hàm số sin x là một đường cong lượn sóng, cắt trục hoành tại các điểm có tọa độ (kπ; 0), với k là số nguyên.

2. Đồ thị hàm số y = cos x:

Tập xác định: R
Tập giá trị: [-1; 1]
Tính tuần hoàn: T = 2π
Tính chẵn lẻ: Hàm số chẵn

Đồ thị hàm số cos x là một đường cong lượn sóng, cắt trục hoành tại các điểm có tọa độ (π/2 + kπ; 0), với k là số nguyên.

3. Đồ thị hàm số y = tan x:

Tập xác định: R \ {π/2 + kπ, k ∈ Z}
Tập giá trị: R
Tính tuần hoàn: T = π
Tính chẵn lẻ: Hàm số lẻ

Đồ thị hàm số tan x có các đường tiệm cận đứng tại các điểm x = π/2 + kπ, với k là số nguyên.

4. Đồ thị hàm số y = cot x:

Tập xác định: R \ {kπ, k ∈ Z}
Tập giá trị: R
Tính tuần hoàn: T = π
Tính chẵn lẻ: Hàm số lẻ

Đồ thị hàm số cot x có các đường tiệm cận đứng tại các điểm x = kπ, với k là số nguyên.

III. Các phép biến đổi đồ thị hàm số lượng giác

Các phép biến đổi đồ thị hàm số lượng giác bao gồm:

Biến đổi theo phương ngang: Dịch chuyển đồ thị sang trái hoặc sang phải.
Biến đổi theo phương dọc: Kéo giãn hoặc nén đồ thị theo phương dọc.
Biến đổi đối xứng: Phản chiếu đồ thị qua trục hoành hoặc trục tung.

IV. Ứng dụng của hàm số lượng giác và đồ thị hàm số lượng giác

Hàm số lượng giác và đồ thị hàm số lượng giác có nhiều ứng dụng trong các lĩnh vực khác nhau, như:

Vật lý: Mô tả các hiện tượng dao động, sóng.
Kỹ thuật: Tính toán các thông số trong các mạch điện xoay chiều, xử lý tín hiệu.
Địa lý: Xác định vị trí, đo đạc khoảng cách.

V. Bài tập vận dụng

Để củng cố kiến thức về lý thuyết hàm số lượng giác và đồ thị hàm số lượng giác, bạn có thể thực hành giải các bài tập sau:

Vẽ đồ thị hàm số y = 2sin x.
Tìm tập xác định và tập giá trị của hàm số y = tan(x + π/4).
Xác định tính chẵn lẻ của hàm số y = cos^2 x.

Hy vọng rằng, với những kiến thức và hướng dẫn trên, bạn sẽ nắm vững lý thuyết hàm số lượng giác và đồ thị hàm số lượng giác, từ đó đạt kết quả tốt trong các kỳ thi và ứng dụng vào thực tế.