Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 1 tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Ở bài viết này, chúng ta sẽ cùng nhau giải quyết các bài tập trong mục 2, trang 32, 33, 34, 35, 36, 37, 38 của SGK Toán 11 tập 1. Hãy cùng bắt đầu!
Trong Hình 1.45, xét đường thẳng \(y = m\left( { - 1 \le m \le 1} \right)\) và đồ thị hàm số \(y = \sin x\).
Trong Hình 1.45, xét đường thẳng \(y = m\left( { - 1 \le m \le 1} \right)\) và đồ thị hàm số \(y = \sin x\).
a) Dựa vào Hình 1.45, cho biết trên đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\), đồ thị hàm số \(y = \sin x\) cắt đường thẳng \(y = m\) tại điểm có hoành độ là giá trị nào.
b) Biểu diễn hoành độ của tất cả các giao điểm của đồ thị hàm số \(y = \sin x\) và đường thẳng \(y = m\) theo hoành độ của giao điểm trong câu a).
Phương pháp giải:
Quan sát hình vẽ để trả lời câu hỏi.
Lời giải chi tiết:
a) Dựa vào Hình 1.45, trên đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\), đồ thị hàm số \(y = \sin x\) cắt đường thẳng \(y = m\) tại điểm có hoành độ là \(a\) và \(\pi - a\).
b) Hoành độ của tất cả các giao điểm lần lượt từ trái sang phải là \( - 3\pi - a;a - 2\pi ; - \pi - a;a;\pi - a;a + 2\pi ;3\pi - a\).
Giải các phương trình sau:
a) \(\sin x = \frac{1}{3};\)
b) \(\sin 2x = - \frac{1}{2};\)
c) \(\sin \left( {x + {{30}^0}} \right) = \frac{{\sqrt 2 }}{2}\).
Phương pháp giải:
\(\begin{array}{l}\sin x = m \Leftrightarrow \sin x = \sin \alpha \\ \Rightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
Lời giải chi tiết:
a)
\(\begin{array}{l}\sin x = \frac{1}{3}\\ \Leftrightarrow \sin x = \sin 0,34\\ \Rightarrow \left[ \begin{array}{l}x = 0,34 + k2\pi \\x = \pi - 0,34 + k2\pi \approx 2,8 + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
Vậy phương trình có các nghiệm là \(x = 0,34 + k2\pi ,x = 2,8 + k2\pi \left( {k \in \mathbb{Z}} \right)\).
b)
\(\begin{array}{l}\sin 2x = - \frac{1}{2}\\ \Leftrightarrow \sin 2x = \sin \left( { - \frac{\pi }{6}} \right)\\ \Rightarrow \left[ \begin{array}{l}x = - \frac{\pi }{6} + k2\pi \\x = \pi - \left( { - \frac{\pi }{6}} \right) + k2\pi = \frac{{7\pi }}{6} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
Vậy phương trình có các nghiệm là \(x = - \frac{\pi }{6} + k2\pi ,x = \frac{{7\pi }}{6} + k2\pi \left( {k \in \mathbb{Z}} \right)\).
c)
\(\begin{array}{l}\sin \left( {x + {{30}^0}} \right) = \frac{{\sqrt 2 }}{2}\\ \Leftrightarrow \sin \left( {x + {{30}^0}} \right) = \sin \left( {{{45}^0}} \right)\\ \Rightarrow \left[ \begin{array}{l}x + {30^0} = {45^0} + k{360^0}\\x + {30^0} = {180^0} - {45^0} + k{360^0} = {135^0} + k{360^0}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}x = {15^0} + k{360^0}\\x = {180^0} - {45^0} - {30^0} + k{360^0} = {105^0} + k{360^0}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
Vậy phương trình có các nghiệm là \(x = {15^0} + k{360^0},x = {105^0} + k{360^0}\left( {k \in \mathbb{Z}} \right)\).
Giải phương trình: \(\sin 4x = - \sin \left( {\pi - x} \right)\).
Phương pháp giải:
\(\begin{array}{l}\sin x = - \sin \alpha \\ \Leftrightarrow \sin x = \sin \left( { - \alpha } \right)\\ \Rightarrow \left[ \begin{array}{l}x = - \alpha + k2\pi \\x = \pi + \alpha + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
Lời giải chi tiết:
\(\begin{array}{l}\sin 4x = - \sin \left( {\pi - x} \right)\\ \Leftrightarrow \sin 4x = \sin \left( { - \pi + x} \right)\\ \Rightarrow \left[ \begin{array}{l}4x = - \pi + x + k2\pi \\x = \pi - \left( { - \pi + x} \right) + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}3x = - \pi + k2\pi \\2x = 2\pi + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}x = - \frac{\pi }{3} + k\frac{{2\pi }}{3}\\x = \pi + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
Vậy phương trình có các nghiệm là \(x = - \frac{\pi }{3} + k\frac{{2\pi }}{3},x = \pi + k\pi \left( {k \in \mathbb{Z}} \right)\).
Giả sử số lượng N của một loài hươu sau t năm được xác định bởi công thức
\(N = 30000 + 20000\sin \left( {\frac{{\pi t}}{{10}}} \right)\)
Xác định năm đầu tiên mà số lượng của loài hươu này bằng 50 nghìn con theo công thức trên.
Phương pháp giải:
Thay N = 50000 vào phương trình. Giải phương trình lượng giác cơ bản để tìm t.
Lời giải chi tiết:
Thay N = 50000 vào phương trình, ta có:
\(\begin{array}{l}30000 + 20000\sin \left( {\frac{{\pi t}}{{10}}} \right) = 50000\\ \Leftrightarrow \sin \left( {\frac{{\pi t}}{{10}}} \right) = 1\\ \Leftrightarrow \sin \left( {\frac{{\pi t}}{{10}}} \right) = \sin \left( {\frac{\pi }{2}} \right)\\ \Rightarrow \frac{{\pi t}}{{10}} = \frac{\pi }{2} + k2\pi \\ \Leftrightarrow t = 5 + k20\left( {k \in \mathbb{Z}} \right)\end{array}\)
Vậy sau 5 năm đầu tiên thì số lượng của loài hươu này bằng 50 nghìn con.
Trong Hình 1.46, xét đường thẳng \(y = m\left( { - 1 \le m \le 1} \right)\) và đồ thị hàm số \(y = \cos x\).

a) Dựa vào Hình 1.46, cho biết trên đoạn \(\left[ {0;\pi } \right]\), đồ thị hàm số \(\cos x = m\) cắt đường thẳng \(y = m\) tại điểm có hoành độ là giá trị nào.
b) Biểu diễn hoành độ của tất cả các giao điểm của đồ thị hàm số \(y = \cos x\) và đường thẳng \(y = m\) theo hoành độ của giao điểm trong câu a).
Phương pháp giải:
Quan sát hình vẽ để trả lời câu hỏi.
Lời giải chi tiết:
a) Dựa vào Hình 1.46, trên đoạn \(\left[ {0;\pi } \right]\), đồ thị hàm số \(\cos x = m\) cắt đường thẳng \(y = m\) tại điểm có hoành độ là \( - a\) và \(a\).
b) Hoành độ của tất cả các giao điểm của đồ thị hàm số \(y = \cos x\) và đường thẳng \(y = m\) lần lượt từ trái sang phải là \( - a - 2\pi ;a - 2\pi ; - a;a; - a + 2\pi ;a + 2\pi \).
Giải các phương trình sau:
a) \(\cos 2x = \cos \frac{\pi }{3};\)
b) \(\cos \left( {x + \frac{\pi }{4}} \right) = - 1;\)
c) \(\cos \left( {x - {{45}^0}} \right) = \frac{{\sqrt 3 }}{2}.\)
Phương pháp giải:
\(\begin{array}{l}\cos x = m\\ \Leftrightarrow \cos x = \cos \alpha \\ \Rightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = - \alpha + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
Lời giải chi tiết:
a)
\(\begin{array}{l}\cos 2x = \cos \frac{\pi }{3}\\ \Rightarrow \left[ \begin{array}{l}2x = \frac{\pi }{3} + k2\pi \\2x = - \frac{\pi }{3} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} + k\pi \\x = - \frac{\pi }{6} + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
Vậy phương trình có các nghiệm là \(x = \frac{\pi }{6} + k\pi ,x = - \frac{\pi }{6} + k\pi \left( {k \in \mathbb{Z}} \right)\)
b)
\(\begin{array}{l}\cos \left( {x + \frac{\pi }{4}} \right) = - 1\\ \Leftrightarrow x + \frac{\pi }{4} = \pi + k2\pi \left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow x = \frac{{3\pi }}{4} + k2\pi \left( {k \in \mathbb{Z}} \right)\end{array}\)
Vậy phương trình có các nghiệm là \(x = \frac{{3\pi }}{4} + k2\pi \left( {k \in \mathbb{Z}} \right)\)
c)
\(\begin{array}{l}\cos \left( {x - {{45}^0}} \right) = \frac{{\sqrt 3 }}{2}\\ \Leftrightarrow \cos \left( {x - {{45}^0}} \right) = \cos \left( {{{30}^0}} \right)\\ \Rightarrow \left[ \begin{array}{l}x - {45^0} = {30^0} + k{360^0}\\x - {45^0} = - {30^0} + k{360^0}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}x = {75^0} + k{360^0}\\x = {15^0} + k{360^0}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
Vậy phương trình có các nghiệm là \(x = {75^0} + k{360^0},x = {15^0} + k{360^0}\left( {k \in \mathbb{Z}} \right)\)
Giải phương trình sau: \(\sin 5x = - \cos \left( {\pi + x} \right).\)
Phương pháp giải:
Đưa phương trình về dạng \(\cos x = \cos \alpha \)\( \Rightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = - \alpha + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
Lời giải chi tiết:
\(\begin{array}{l}\sin 5x = - \cos \left( {\pi + x} \right)\\ \Leftrightarrow \cos \left( {\frac{\pi }{2} - 5x} \right) = \cos \left( {\pi + x} \right)\\ \Rightarrow \left[ \begin{array}{l}\frac{\pi }{2} - 5x = \pi + x + k2\pi \\\frac{\pi }{2} - 5x = - \pi - x + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l} - 6x = \frac{\pi }{2} + k2\pi \\ - 4x = - \frac{{3\pi }}{2} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}x = - \frac{\pi }{{12}} - k\frac{\pi }{3}\\x = \frac{{3\pi }}{8} - k\frac{\pi }{2}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
Vậy phương trình có các nghiệm là \(x = - \frac{\pi }{{12}} - k\frac{\pi }{3},x = \frac{{3\pi }}{8} - k\frac{\pi }{2}\)
Cường độ dòng điện i (ampe) qua một mạch điện xoay chiều được tính bởi công thức \(i = 10\sqrt 2 \cos \left( {100\pi t} \right),\) trong đó t là thời gian tính bằng giây. Xác định thời điểm đầu tiên cường độ dòng điện bằng 10 ampe.
Phương pháp giải:
Thay i = 10 vào công thức. Giải phương trình lượng giác cơ bản để tìm t.
Lời giải chi tiết:
Thay i = 10 vào công thức, ta có:
\(\begin{array}{l}10\sqrt 2 \cos \left( {100\pi t} \right) = 10\\ \Leftrightarrow \cos \left( {100\pi t} \right) = \frac{1}{{\sqrt 2 }}\\ \Leftrightarrow \cos \left( {100\pi t} \right) = \cos \left( {\frac{\pi }{4}} \right)\\ \Rightarrow \left[ \begin{array}{l}100\pi t = \frac{\pi }{4} + k2\pi \\100\pi t = - \frac{\pi }{4} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}t = \frac{1}{{400}} + \frac{k}{{50}}\\t = - \frac{1}{{400}} + \frac{k}{{50}}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
Vậy thời điểm đầu tiên cường độ dòng điện bằng 10 ampe là \(\frac{1}{{400}}\) giây.
Trong Hình 1.47, xét đường thẳng \(y = m\) và đồ thị hàm số \(y = \tan x\).

a) Dựa vào Hình 1.47, cho biết trên đoạn \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\), đồ thị hàm số \(y = \tan x\) cắt đường thẳng \(y = m\) tại điểm có hoành độ là giá trị nào.
b) Biểu diễn hoành độ của tất cả các giao điểm của đồ thị hàm số \(y = \tan x\) và đường thẳng \(y = m\) theo hoành độ của giao điểm trong câu a).
Phương pháp giải:
Quan sát hình vẽ để trả lời.
Lời giải chi tiết:
a) Dựa vào Hình 1.47, trên đoạn \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\), đồ thị hàm số \(y = \tan x\) cắt đường thẳng \(y = m\) tại điểm có hoành độ là \(a\).
b) Hoành độ của tất cả các giao điểm của đồ thị hàm số \(y = \tan x\) và đường thẳng \(y = m\) lần lượt từ trái sang phải là \(a - 2\pi ,a - \pi ,a,a + \pi ,a + 2\pi \).
Giải các phương trình sau:
a) \(\tan 3x = 1;\)
b) \(\tan 4x = - 1,5;\)
c) \(\tan \left( {x + {{15}^0}} \right) = - \sqrt 3 .\)
Phương pháp giải:
\(\begin{array}{l}\tan x = m\\ \Leftrightarrow \tan x = \tan \alpha \\ \Leftrightarrow x = \alpha + k\pi \left( {k \in \mathbb{Z}} \right)\end{array}\)
Lời giải chi tiết:
a)
\(\begin{array}{l}\tan 3x = 1\\ \Leftrightarrow \tan 3x = \tan \frac{\pi }{4}\\ \Leftrightarrow 3x = \frac{\pi }{4} + k\pi \left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow x = \frac{\pi }{{12}} + k\frac{\pi }{3}\left( {k \in \mathbb{Z}} \right)\end{array}\)
Vậy phương trình có nghiệm là \(x = \frac{\pi }{{12}} + k\frac{\pi }{3}\left( {k \in \mathbb{Z}} \right)\)
b) Gọi a là góc lượng giác thuộc khoảng \(\left( {0;\pi } \right)\) thỏa mãn \(\tan 4x = - 1,5\)
\(\begin{array}{l}\tan 4x = \tan a\\ \Leftrightarrow 4x = a + k\pi \left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow x = \frac{a}{4} + k\frac{\pi }{4}\left( {k \in \mathbb{Z}} \right)\end{array}\)
Vậy phương trình có nghiệm là \(x = \frac{a}{4} + k\frac{\pi }{4}\left( {k \in \mathbb{Z}} \right)\)
c)
\(\begin{array}{l}\tan \left( {x + {{15}^0}} \right) = - \sqrt 3 \\ \Leftrightarrow \tan \left( {x + {{15}^0}} \right) = \tan \left( { - {{60}^0}} \right)\\ \Leftrightarrow x + {15^0} = - {60^0} + k{180^0}\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow x = - {75^0} + k{180^0}\left( {k \in \mathbb{Z}} \right)\end{array}\)
Vậy phương trình có nghiệm là \(x = - {75^0} + k{180^0}\left( {k \in \mathbb{Z}} \right)\)
Một người dẫn em gái của mình đến công viên để chơi xích đu. Lực đẩy theo phương ngang F (N) mà người đó dùng để đẩy em gái trong trò chơi này được xác định bởi công thức \(F = mg\tan \theta \), trong đó m (kg) là khối lượng của em gái, g là gia tốc trọng trường và \(\theta \) là góc tạo bởi xích đu khi bắt đầu được đẩy với phương thẳng đứng (Hình 1.49) (nguồn: https://www.khanacademy.org/science/physics/centripetal-force-and-gravitation/centripetal-forces/v/mass-swiging-in-a-horizontal-circle). Xác định góc \(\theta \) khi \(F = 400\sqrt 3 \)N, m = 40 kg và g = 10 m/s2.

Phương pháp giải:
Thay \(F = 400\sqrt 3 \), m = 40 và g = 10 vào công thức. Giải phương trình lượng giác cơ bản để tìm \(\theta \).
Lời giải chi tiết:
\(\begin{array}{l}400\sqrt 3 = 40.10.\tan \theta \\ \Leftrightarrow \tan \theta = \sqrt 3 \\ \Leftrightarrow \tan \theta = \tan {60^0}\\ \Leftrightarrow \theta = {60^0} + k{180^0}\left( {k \in \mathbb{Z}} \right)\end{array}\)
Vậy \(\theta = {60^0}\)
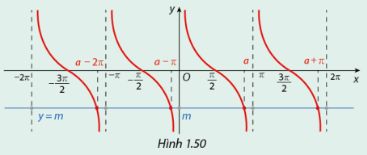
Trong Hình 1.50, xét đường thẳng \(y = m\)và đồ thị hàm số \(y = \cot x\).

a) Dựa vào Hình 1.50, cho biết trên đoạn \(\left( {0;\pi } \right)\), đồ thị hàm số \(y = \cot x\) cắt đường thẳng \(y = m\) tại điểm có hoành độ là giá trị nào.
b) Biểu diễn hoành độ của tất cả các giao điểm của đồ thị hàm số \(y = \cot x\) và đường thẳng \(y = m\) theo hoành độ của giao điểm trong câu a).
Phương pháp giải:
Quan sát hình vẽ để trả lời.
Lời giải chi tiết:
a) Dựa vào Hình 1.50, trên đoạn \(\left( {0;\pi } \right)\), đồ thị hàm số \(y = \cot x\) cắt đường thẳng \(y = m\) tại điểm có hoành độ là \(a\).
b) Hoành độ của tất cả các giao điểm của đồ thị hàm số \(y = \cot x\) và đường thẳng \(y = m\) lần lượt từ trái sang phải là \(a - 2\pi ,a - \pi ,a,a + \pi \).
Giải các phương trình sau:
a) \(\cot 2x = - 1;\)
b) \(\cot 6x = 4;\)
c) \(\cot \left( {x - {{45}^0}} \right) = \sqrt 3 .\)
Phương pháp giải:
\(\begin{array}{l}\cot a = m \Leftrightarrow \cot a = \cot b\\ \Leftrightarrow a = b + k\pi \left( {k \in \mathbb{Z}} \right)\end{array}\)
Lời giải chi tiết:
a)
\(\begin{array}{l}\cot 2x = - 1\\ \Leftrightarrow \cot 2x = \cot \left( { - \frac{\pi }{4}} \right)\\ \Leftrightarrow 2x = - \frac{\pi }{4} + k\pi \left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow x = - \frac{\pi }{8} + k\frac{\pi }{2}\left( {k \in \mathbb{Z}} \right)\end{array}\)
Vậy phương trình có nghiệm là \(x = - \frac{\pi }{8} + k\frac{\pi }{2}\left( {k \in \mathbb{Z}} \right)\)
b) Gọi a là góc lượng giác thuộc khoảng \(\left( {0;\pi } \right)\) thỏa mãn \(\cot 6x = 4\)
\(\begin{array}{l}\cot 6x = \cot a\\ \Leftrightarrow 6x = a + k\pi \left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow x = \frac{a}{6} + k\frac{\pi }{6}\left( {k \in \mathbb{Z}} \right)\end{array}\)
Vậy phương trình có nghiệm là \(x = \frac{a}{6} + k\frac{\pi }{6}\left( {k \in \mathbb{Z}} \right)\)
c)
\(\begin{array}{l}\cot \left( {x - {{45}^0}} \right) = \sqrt 3 \\ \Leftrightarrow \cot \left( {x - {{45}^0}} \right) = \cot \left( {{{30}^0}} \right)\\ \Leftrightarrow x - {45^0} = {30^0} + k{180^0}\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow x = {75^0} + k{180^0}\left( {k \in \mathbb{Z}} \right)\end{array}\)
Vậy phương trình có nghiệm là \(x = {75^0} + k{180^0}\left( {k \in \mathbb{Z}} \right)\)
Mục 2 của SGK Toán 11 tập 1 thường tập trung vào các kiến thức về phép biến hình, bao gồm phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm. Việc nắm vững các tính chất và ứng dụng của các phép biến hình này là rất quan trọng để giải quyết các bài toán hình học một cách hiệu quả.
Phép tịnh tiến là phép biến hình giữ nguyên mọi điểm, di chuyển chúng theo một vectơ cho trước. Để giải các bài toán liên quan đến phép tịnh tiến, cần xác định đúng vectơ tịnh tiến và áp dụng công thức biến đổi tọa độ.
Phép quay là phép biến hình biến mỗi điểm thành một điểm khác sao cho khoảng cách từ điểm đó đến tâm quay không đổi và góc giữa hai đoạn thẳng nối điểm ban đầu và điểm sau khi quay với tâm quay là một góc cố định. Việc xác định tâm quay và góc quay là chìa khóa để giải quyết các bài toán về phép quay.
Phép đối xứng trục là phép biến hình biến mỗi điểm thành một điểm khác sao cho đường trung trực của đoạn thẳng nối hai điểm là trục đối xứng. Để tìm ảnh của một điểm qua phép đối xứng trục, cần tìm giao điểm của đường thẳng vuông góc với trục đối xứng và đi qua điểm đó với trục đối xứng.
Phép đối xứng tâm là phép biến hình biến mỗi điểm thành một điểm khác sao cho tâm của đoạn thẳng nối hai điểm là tâm đối xứng. Việc tìm tọa độ tâm đối xứng là bước quan trọng để giải quyết các bài toán về phép đối xứng tâm.
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 2, trang 32, 33, 34, 35, 36, 37, 38 SGK Toán 11 tập 1:
Để giải các bài tập về phép biến hình một cách nhanh chóng và chính xác, các em cần:
Ngoài ra, các em cũng nên luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau và rèn luyện kỹ năng giải toán.
Hy vọng rằng với lời giải chi tiết và những lưu ý quan trọng trên, các em sẽ tự tin hơn trong việc giải các bài tập về phép biến hình trong SGK Toán 11 tập 1. Chúc các em học tập tốt và đạt kết quả cao!