Bài 8.26 trang 79 SGK Toán 11 tập 2 thuộc chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài tập này đòi hỏi học sinh phải nắm vững kiến thức về đạo hàm, cực trị và các tính chất của hàm số.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh hiểu rõ phương pháp giải và tự tin làm bài tập. Chúng tôi luôn cập nhật lời giải mới nhất và chính xác nhất để hỗ trợ học sinh trong quá trình học tập.
Cho hình lăng trụ tứ giác đều ABCD.A’B’C’D’ có cạnh đáy bằng a
Đề bài
Cho hình lăng trụ tứ giác đều ABCD.A’B’C’D’ có cạnh đáy bằng a. Gọi M, N, P lần lượt là trung điểm của AD, DC, A’D’. Tính khoảng cách giữa hai mặt phẳng (MNP) và (ACC’).
Phương pháp giải - Xem chi tiết
Khoảng cách giữa 2 mặt phẳng song song là khoảng cách từ 1 điểm bất kì của mặt này đến mặt phẳng kia.
Lời giải chi tiết
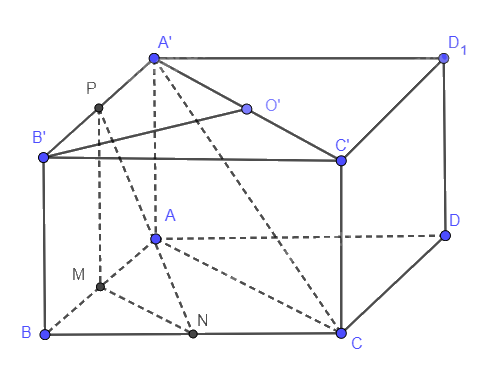
Ta có: MN // AC, MP // AA’
Nên (MNP) // (ACC’)
Nên khoảng cách cần tìm bằng khoảng cách giữa P và (ACC’) và bằng một nửa khoảng cách giữa B và (ACC’)
B’O’ vuông góc với A’C’, B’C’ vuông góc với CC’
Suy ra B’O’ vuông góc với (ACC’)
Nên khoảng cách giữa B và (ACC’) là B’O’ = 1/2B’D’ = \(\frac{{a\sqrt 2 }}{2}\)
Vậy khoảng cách cần tìm bằng \(\frac{{a\sqrt 2 }}{4}\).
Bài 8.26 trang 79 SGK Toán 11 tập 2 yêu cầu chúng ta khảo sát hàm số và tìm các điểm cực trị. Để giải bài toán này, chúng ta cần thực hiện các bước sau:
Giả sử hàm số cần khảo sát là f(x) = x3 - 3x2 + 2.
Vậy x = 0 là điểm cực đại, x = 2 là điểm cực tiểu.
| x | -∞ | 0 | 2 | +∞ | |
|---|---|---|---|---|---|
| f'(x) | + | 0 | - | 0 | + |
| f(x) | 2 | -2 |
Từ bảng biến thiên, ta thấy hàm số đạt cực đại tại x = 0 với giá trị là f(0) = 2 và đạt cực tiểu tại x = 2 với giá trị là f(2) = -2.
Khi giải các bài toán về khảo sát hàm số, cần chú ý đến các bước thực hiện và sử dụng đúng các công thức, định lý. Việc lập bảng biến thiên giúp ta hình dung rõ hơn về sự biến thiên của hàm số và các điểm cực trị.
Ngoài ra, cần rèn luyện thêm nhiều bài tập khác để nắm vững kiến thức và kỹ năng giải toán. Giaitoan.edu.vn cung cấp một kho bài tập phong phú, đa dạng, giúp bạn luyện tập và nâng cao khả năng giải toán.
Để hiểu sâu hơn về đạo hàm và ứng dụng của đạo hàm, bạn có thể tham khảo thêm các tài liệu sau:
Việc nắm vững kiến thức về đạo hàm và ứng dụng của đạo hàm là rất quan trọng trong chương trình Toán 11 và là nền tảng cho các kiến thức nâng cao hơn trong các lớp học tiếp theo. Hãy dành thời gian ôn tập và luyện tập thường xuyên để đạt kết quả tốt nhất.
Bài 8.26 trang 79 SGK Toán 11 tập 2 là một bài tập điển hình để rèn luyện kỹ năng khảo sát hàm số. Hy vọng với lời giải chi tiết và các lưu ý quan trọng trên, bạn sẽ tự tin giải quyết bài toán này và các bài toán tương tự.
Chúc bạn học tốt!