Bài 8.27 trang 79 SGK Toán 11 tập 2 thuộc chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài tập này đòi hỏi học sinh phải nắm vững kiến thức về các công thức đạo hàm cơ bản và cách áp dụng chúng vào giải quyết các bài toán cụ thể.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh hiểu rõ bản chất của bài toán và tự tin giải các bài tập tương tự. Chúng tôi luôn cập nhật lời giải mới nhất và chính xác nhất để hỗ trợ tối đa cho quá trình học tập của bạn.
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b.
Đề bài
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b. Tính khoảng cách giữa hai đường thẳng BB’ và AC’.
Phương pháp giải - Xem chi tiết
Chọn (P) chứa a và song song với b. Khi đó khoảng cách a và b là khoảng cách giữa b và (P).
Lời giải chi tiết
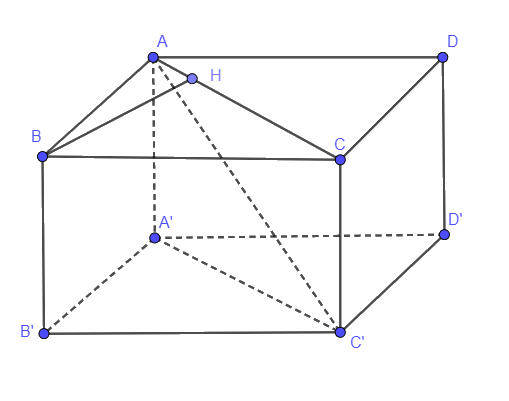
Ta có: CC’ // BB’ nên BB’ // (ACC’A’)
Suy ra khoảng cách giữa BB’ và AC’ là khoảng cách giữa BB’ và (ACC’A’) hay khoảng cách giữa B là (ACC’A’)
Kẻ BH vuông góc với AC
\(\begin{array}{l}AC = \sqrt {{a^2} + {b^2}} \\AB.BC = BH.AC\\ \Leftrightarrow BH = \frac{{ab}}{{\sqrt {{a^2} + {b^2}} }}\end{array}\)
Bài 8.27 trang 79 SGK Toán 11 tập 2 yêu cầu học sinh giải một bài toán cụ thể liên quan đến việc tìm cực trị của hàm số. Để giải bài toán này, chúng ta cần thực hiện các bước sau:
Giả sử hàm số f(x) = x3 - 3x2 + 2. Ta thực hiện các bước sau:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | ↗ | ↘ | ↗ |
Bước 5: Kết luận: Hàm số đạt cực đại tại x = 0, f(0) = 2 và đạt cực tiểu tại x = 2, f(2) = -2.
Việc tìm cực trị của hàm số có nhiều ứng dụng trong thực tế, chẳng hạn như:
Để nắm vững kiến thức về đạo hàm và ứng dụng của đạo hàm, học sinh cần luyện tập thường xuyên các bài tập khác nhau. Giaitoan.edu.vn cung cấp một kho bài tập phong phú, đa dạng, giúp học sinh rèn luyện kỹ năng giải toán một cách hiệu quả.
Khi giải bài toán cực trị, học sinh cần lưu ý một số điểm sau:
Ngoài ra, học sinh cũng nên tham khảo các tài liệu học tập khác, chẳng hạn như sách giáo khoa, sách bài tập, các trang web học toán trực tuyến để có thêm kiến thức và kỹ năng giải toán.
Bài 8.27 trang 79 SGK Toán 11 tập 2 là một bài tập quan trọng, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Hy vọng với lời giải chi tiết và những lưu ý trên, các bạn học sinh sẽ tự tin giải bài tập này và đạt kết quả tốt trong môn Toán.
Việc hiểu rõ bản chất của bài toán và áp dụng đúng các công thức, phương pháp giải là chìa khóa để thành công. Hãy luyện tập thường xuyên và đừng ngần ngại tìm kiếm sự giúp đỡ khi gặp khó khăn. Chúc các bạn học tốt!