Chào mừng bạn đến với bài học về Lý thuyết Giới hạn của dãy số, một trong những chủ đề quan trọng của chương trình Toán 11. Bài học này được thiết kế để giúp bạn hiểu rõ các khái niệm cơ bản, tính chất và ứng dụng của giới hạn dãy số theo chương trình SGK Toán 11.
Tại giaitoan.edu.vn, chúng tôi cung cấp tài liệu học tập đầy đủ, bài giảng chi tiết và bài tập thực hành đa dạng để bạn có thể tự tin chinh phục môn Toán.
I. Giới hạn hữu hạn của dãy số
I. Giới hạn hữu hạn của dãy số
1. Dãy số có giới hạn bằng 0
- Dãy số \(\left( {{u_n}} \right)\)có giới hạn 0 khi n dần tới dương vô cực, nếu \(\left| {{u_n}} \right|\) có thể nhỏ hơn một số dương bé tùy ý , kể tử một số hạng nào đó trở đi.
Kí hiệu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = 0\) hay \({u_n} \to 0\) khi \(n \to + \infty \) hay \(\lim {u_n} = 0\).
* Chú ý:
+ \(\lim \frac{1}{{{n^k}}} = 0,k \in \mathbb{Z}.\)
+ Nếu \(\left| q \right| < 1\) thì \(\lim {q^n} = 0\)
2. Dãy số có giới hạn hữu hạn
Ta nói dãy số \(\left( {{u_n}} \right)\) có giới hạn là số thực a khi n dần tới dương vô cực, nếu \(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - a} \right) = 0\), kí hiệu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a\) hay \({u_n} \to a\)khi \(n \to + \infty \).
* Chú ý: Nếu \({u_n} = c\) (c là hằng số) thì \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = c\)
3. Định lí về giới hạn hữu hạn
Cho \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a,\mathop {\lim }\limits_{n \to + \infty } {v_n} = b\) và c là hằng số thì
4. Tổng của cấp số nhân lùi vô hạn
Cấp số nhân \(\left( {{u_n}} \right)\) có công bội q thỏa mãn \(\left| q \right| < 1\) được gọi là cấp số nhân lùi vô hạn.
Tổng của cấp số nhân lùi vô hạn là:
\(S = \frac{{{u_1}}}{{1 - q}}\left( {\left| q \right| < 1} \right)\)
II. Giới hạn vô cực
- Dãy số \(\left( {{u_n}} \right)\) được gọi là có giới hạn \( + \infty \)khi \(n \to + \infty \) nếu \({u_n}\) có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi, kí hiệu \(\mathop {\lim }\limits_{x \to + \infty } {u_n} = + \infty \) hay \({u_n} \to + \infty \) khi \(n \to + \infty \).
- Dãy số \(\left( {{u_n}} \right)\) được gọi là có giới hạn \( - \infty \)khi \(n \to + \infty \) nếu \(\mathop {\lim }\limits_{x \to + \infty } \left( { - {u_n}} \right) = + \infty \), kí hiệu \(\mathop {\lim }\limits_{x \to + \infty } {u_n} = - \infty \) hay \({u_n} \to - \infty \) khi \(n \to + \infty \).
*Nhận xét:
\(\begin{array}{l}a,\lim {n^k} = + \infty ,k \in \mathbb{N},k \ge 1.\\b,\lim {q^n} = + \infty ;q \in \mathbb{R},q > 1.\end{array}\)
* Chú ý:
Nếu \(\mathop {\lim }\limits_{x \to + \infty } {u_n} = a\)và \(\mathop {\lim }\limits_{x \to + \infty } {v_n} = + \infty \)(hoặc\(\mathop {\lim }\limits_{x \to + \infty } {v_n} = - \infty \))thì \(\mathop {\lim }\limits_{n \to + \infty } (\frac{{{u_n}}}{{{v_n}}}) = 0\).
Nếu \(\mathop {\lim }\limits_{x \to + \infty } {u_n} = a > 0\) và \(\mathop {\lim }\limits_{x \to + \infty } {v_n} = 0,{v_n} > 0\)thì \(\mathop {\lim }\limits_{n \to + \infty } (\frac{{{u_n}}}{{{v_n}}}) = + \infty \).
Nếu \(\mathop {\lim }\limits_{x \to + \infty } {u_n} = a > 0\) và \(\mathop {\lim }\limits_{x \to + \infty } {v_n} = 0,{v_n} < 0\)thì \(\mathop {\lim }\limits_{n \to + \infty } (\frac{{{u_n}}}{{{v_n}}}) = - \infty \).
Nếu \(\mathop {\lim }\limits_{x \to + \infty } {v_n} = a > 0\) và \(\mathop {\lim }\limits_{x \to + \infty } {u_n} = + \infty \)thì \(\mathop {\lim }\limits_{n \to + \infty } ({u_n}.{v_n}) = + \infty \).
Nếu \(\mathop {\lim }\limits_{x \to + \infty } {v_n} = a < 0\) và \(\mathop {\lim }\limits_{x \to + \infty } {u_n} = + \infty \)thì \(\mathop {\lim }\limits_{n \to + \infty } ({u_n}.{v_n}) = - \infty \)
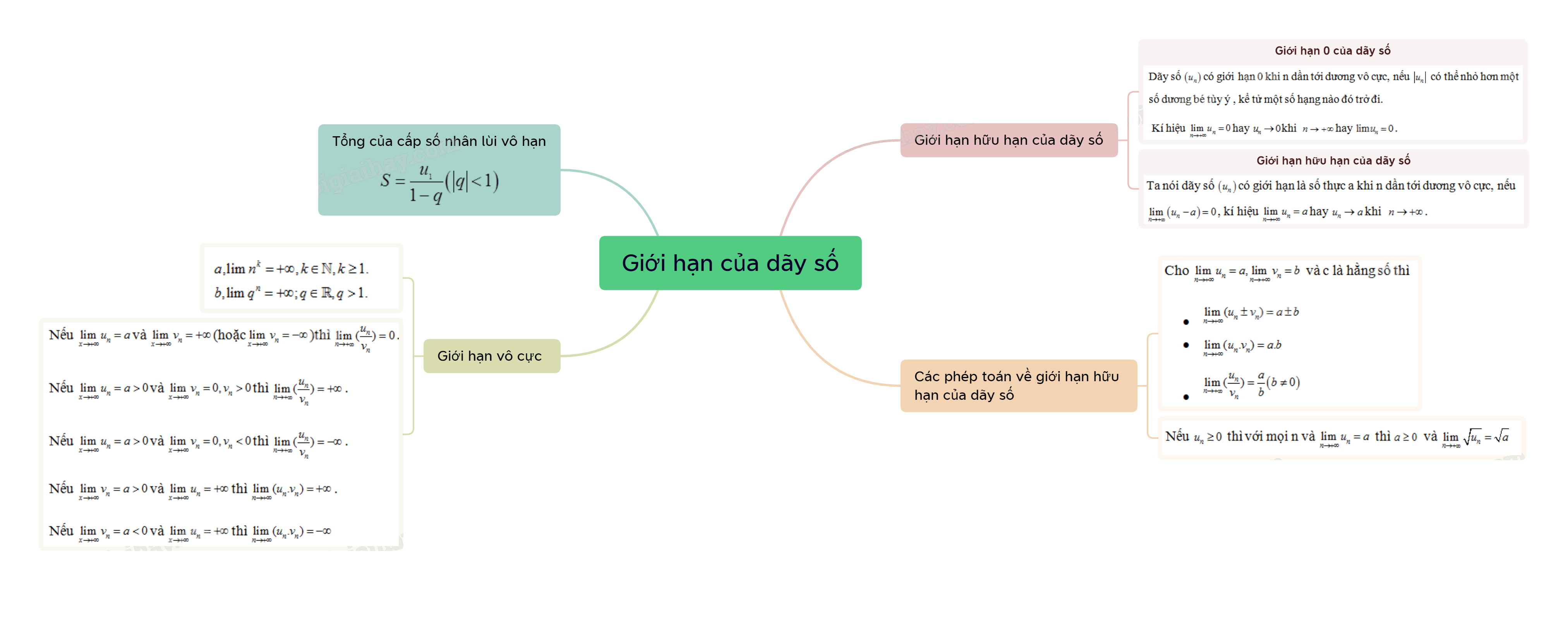
Giới hạn của dãy số là một khái niệm nền tảng trong giải tích, đóng vai trò quan trọng trong việc xây dựng các khái niệm phức tạp hơn như đạo hàm và tích phân. Trong chương trình Toán 11, học sinh bắt đầu làm quen với khái niệm này thông qua việc tìm hiểu về giới hạn của dãy số thực.
Một dãy số là một hàm số f: ℕ → ℝ, tức là một quy tắc xác định một số thực f(n) cho mỗi số tự nhiên n. Dãy số thường được ký hiệu là (un), trong đó un = f(n).
Dãy số (un) được gọi là có giới hạn L nếu với mọi số dương ε (epsilon) nhỏ tùy ý, tồn tại một số tự nhiên N sao cho với mọi n > N, ta có |un - L| < ε. Ký hiệu: limn→∞ un = L.
Trong đó:
Có ba dạng giới hạn chính của dãy số:
Giới hạn dãy số có các tính chất sau:
Ví dụ 1: Tìm giới hạn của dãy số un = 1/n.
Ta có: limn→∞ 1/n = 0.
Ví dụ 2: Tìm giới hạn của dãy số un = n2.
Ta có: limn→∞ n2 = +∞.
Giới hạn dãy số có nhiều ứng dụng trong toán học và các lĩnh vực khác, bao gồm:
Để củng cố kiến thức về giới hạn dãy số, bạn có thể thực hành các bài tập sau:
Hy vọng bài học này đã giúp bạn hiểu rõ hơn về Lý thuyết Giới hạn của dãy số - SGK Toán 11. Chúc bạn học tập tốt!