Bài 4.31 trang 124 SGK Toán 11 tập 1 là một bài toán quan trọng trong chương trình học Toán 11, tập trung vào việc ứng dụng kiến thức về vectơ vào giải quyết các bài toán hình học không gian. Bài toán này đòi hỏi học sinh phải nắm vững các khái niệm về vectơ, phép toán vectơ và khả năng tư duy logic để tìm ra lời giải chính xác.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 4.31 trang 124 SGK Toán 11 tập 1, giúp bạn hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hình hộp ABCD.A'B'C'D'. Gọi M, N, P lần lượt là các điểm nằm trên AA', AB, DC sao cho \(\frac{{AM}}{{AA'}} = \frac{{AN}}{{AB}} = \frac{{DP}}{{DC}} = \frac{1}{3}\).
Đề bài
Cho hình hộp ABCD.A'B'C'D'. Gọi M, N, P lần lượt là các điểm nằm trên AA', AB, DC sao cho \(\frac{{AM}}{{AA'}} = \frac{{AN}}{{AB}} = \frac{{DP}}{{DC}} = \frac{1}{3}\).
a) Chứng minh mặt phẳng (MNP) song song với (A'BC).
b) Gọi Q là giao điểm của AC' với (MNP). Xét vị trí tương đối của MQ và A'C.
Phương pháp giải - Xem chi tiết
a) (P) chứa 2 đường thẳng cắt nhau lần lượt song song với (Q) thì (P) // (Q).
b) Tìm giao điểm của đường thẳng a và mặt phẳng (P):
+ Bước 1: Chọn 1 mặt phẳng (Q) chứa a. Tìm giao tuyến d của (P) và (Q)
+ Bước 2: Tìm giao điểm I của a và d. I chính là giao điểm của a và (P).
Lời giải chi tiết
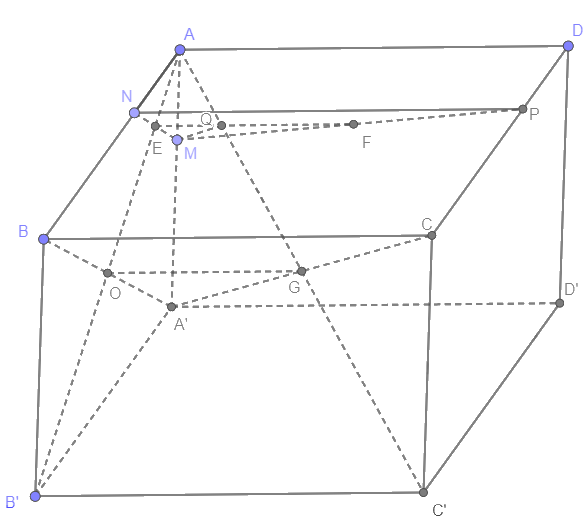
a) Xét tam giác ABA' có \(\frac{{AM}}{{AA'}} = \frac{{AN}}{{AB}} = \frac{1}{3}\) nên MN // A'B. Suy ra MN // (A'BC) (1)
Xét hình bình hành ABCD có \(\frac{{AN}}{{AB}} = \frac{{DP}}{{DC}} = \frac{1}{3}\) nên NP // BC. Suy ra NP // (A'BC) (2)
Từ (1), (2) suy ra (MNP) // (A'BC)
b) Trong (ABB'A'), gọi E là giao điểm của AB' và MN
Suy ra E là điểm chung của (AB'C') và (MNP). Mà NP // B'C' (cùng // BC)
Qua E kẻ đường thẳng d song song với NP và B'C', cắt EP tại F. Suy ra EF là giao tuyến của (MNP) và (AB'C')
Trong (AB'C'), gọi Q là giao điểm của EF và AC'
Vậy Q là giao điểm của AC' và (MNP)
Trong (ABB'A'), gọi O là giao điểm của A'B và AB'
Xét tam giác ABO có NE // BO nên \(\frac{{AN}}{{AB}} = \frac{{AE}}{{AO}} = \frac{1}{3}\)
Ta có: AA' // CC' (cùng // BB') và AA' = CC' (cùng bằng BB') nên ACC'A' là hình bình hành
Trong (AA'C'C), gọi G là giao điểm của AC' và A'C. Suy ra G là trung điểm của AC' và A'C
Xét tam giác AB'C' có O, G là trung điểm của AB', AC' nên OG // B'C'. Suy ra OG // NQ \( \Rightarrow \frac{{AE}}{{AO}} = \frac{{AQ}}{{AG}} = \frac{1}{3}\)
Xét tam giác AA'G có: \(\frac{{AM}}{{AA'}} = \frac{{AQ}}{{AG}} = \frac{1}{3} \Rightarrow MQ\,{\rm{// }}A'G\) hay MQ // A'C.
Bài 4.31 trang 124 SGK Toán 11 tập 1 thường liên quan đến việc xác định mối quan hệ giữa các vectơ trong không gian, ví dụ như chứng minh ba điểm thẳng hàng, hai đường thẳng song song hoặc đồng phẳng. Để giải bài toán này, học sinh cần:
Đề bài: Cho bốn điểm A, B, C, D. Chứng minh rằng bốn điểm này đồng phẳng.
Lời giải:
Giải thích: Hỗn tích của ba vectơ bằng 0 khi và chỉ khi ba vectơ đó đồng phẳng. Điều này có nghĩa là vectơ AD có thể biểu diễn được dưới dạng tổ hợp tuyến tính của hai vectơ AB và AC, do đó bốn điểm A, B, C, D nằm trên cùng một mặt phẳng.
Ngoài bài toán chứng minh bốn điểm đồng phẳng, Bài 4.31 trang 124 SGK Toán 11 tập 1 còn có thể xuất hiện các dạng bài tập khác như:
Để giải quyết các dạng bài tập này, học sinh cần nắm vững các kiến thức sau:
Để củng cố kiến thức và kỹ năng giải bài tập về vectơ, bạn có thể luyện tập thêm với các bài tập tương tự trong SGK Toán 11 tập 1 và các tài liệu tham khảo khác. Giaitoan.edu.vn cung cấp một kho bài tập phong phú, đa dạng với lời giải chi tiết, giúp bạn tự tin chinh phục môn Toán 11.
Bảng tổng hợp các công thức vectơ quan trọng:
| Công thức | Mô tả |
|---|---|
| a + b | Phép cộng vectơ |
| a - b | Phép trừ vectơ |
| k.a | Phép nhân vectơ với một số thực |
| a.b | Tích vô hướng của hai vectơ |
| [a, b, c] | Hỗn tích của ba vectơ |
Hy vọng với những phân tích và lời giải chi tiết trên, bạn đã hiểu rõ hơn về Bài 4.31 trang 124 SGK Toán 11 tập 1. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!