Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 của giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 1 trang 115 và 116 sách giáo khoa Toán 11 tập 1.
Mục tiêu của chúng tôi là giúp các em hiểu rõ kiến thức, nắm vững phương pháp giải và tự tin làm bài tập. Hãy cùng bắt đầu nhé!
Cho mặt phẳng \(\left( \alpha \right)\) và đường thẳng \(\Delta \) cắt \(\left( \alpha \right)\). Lấy M là điểm bất kì trong không gian. Qua M, vẽ đường thẳng d song song với \(\Delta \). Hỏi d và \(\left( \alpha \right)\) có điểm chung hay không?
Cho mặt phẳng \(\left( \alpha \right)\) và đường thẳng \(\Delta \) cắt \(\left( \alpha \right)\). Lấy M là điểm bất kì trong không gian. Qua M, vẽ đường thẳng d song song với \(\Delta \). Hỏi d và \(\left( \alpha \right)\) có điểm chung hay không?
Phương pháp giải:
Chứng minh phản chứng (Giả sử d và \(\left( \alpha \right)\) không có điểm chung).
Lời giải chi tiết:
Giả sử d và \(\left( \alpha \right)\) không có điểm chung nên d // \(\left( \alpha \right)\)
\(\Delta \)// d nên \(\Delta \)// \(\left( \alpha \right)\)
Mà \(\Delta \) cắt \(\left( \alpha \right)\) (Mâu thuẫn)
Vậy d và \(\left( \alpha \right)\) có điểm chung.
Cho hình hộp ABCD.A'B'C'D'. Gọi O là giao điểm hai đường chéo AC và BD. Tìm hình chiếu song song của điểm O trên mặt phẳng (A'B'C'D') theo phương AA'.
Phương pháp giải:
Kẻ đường thẳng đi qua O, song song với AA' và cắt (A'B'C'D') tại điểm O'. O' là hình chiếu song song của O.
Lời giải chi tiết:
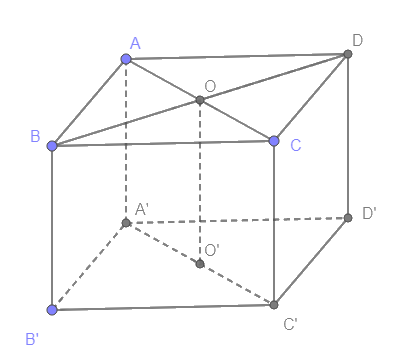
Gọi O' là trung điểm của A'C'
Do ABCD là hình bình hành, O là giao điểm của AC và BD nên O là trung điểm của AC và BD
Ta có AA' // CC' (cùng // BB') và AA' = CC' (cùng = BB') nên ACC'A' là hình bình hành
\( \Rightarrow \)OO' là đường trung bình của hình bình hành ACC'A' nên OO' // AA'
Ta lại có OO' cắt (A'B'C'D') tại O'
Vậy O' là hình chiếu song song của O trên mặt phẳng (A'B'C'D') theo phương AA'.
Mục 1 của chương trình Toán 11 tập 1 thường tập trung vào các kiến thức cơ bản về hàm số, bao gồm định nghĩa hàm số, tập xác định, tập giá trị, và các tính chất của hàm số. Việc nắm vững những kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo.
Bài tập 1 thường yêu cầu xác định xem một biểu thức có phải là hàm số hay không. Để giải bài tập này, các em cần nhớ lại định nghĩa hàm số: một quan hệ giữa hai tập hợp A và B được gọi là hàm số nếu với mỗi phần tử x thuộc A, chỉ có duy nhất một phần tử y thuộc B tương ứng.
Ví dụ:
Bài tập 2 thường yêu cầu tìm tập xác định của hàm số. Tập xác định của hàm số là tập hợp tất cả các giá trị x mà hàm số có nghĩa. Để tìm tập xác định, các em cần xác định các điều kiện để hàm số có nghĩa, ví dụ như mẫu số khác 0, căn thức không âm, logarit có cơ số lớn hơn 0 và khác 1, v.v.
Ví dụ:
Hàm số y = 1/(x-2) có tập xác định là D = R \ {2} (tập hợp tất cả các số thực trừ 2).
Bài tập 3 thường yêu cầu tìm tập giá trị của hàm số. Tập giá trị của hàm số là tập hợp tất cả các giá trị y mà hàm số có thể nhận được. Để tìm tập giá trị, các em có thể sử dụng các phương pháp như xét đạo hàm, tìm giá trị lớn nhất và nhỏ nhất của hàm số, hoặc sử dụng các tính chất của hàm số.
Ví dụ:
Hàm số y = x2 có tập giá trị là [0, +∞) (tập hợp tất cả các số thực không âm).
Bài tập 4 có thể yêu cầu xét tính chẵn, lẻ của hàm số. Một hàm số được gọi là chẵn nếu f(-x) = f(x) với mọi x thuộc tập xác định. Một hàm số được gọi là lẻ nếu f(-x) = -f(x) với mọi x thuộc tập xác định.
Ví dụ:
Ngoài sách giáo khoa, các em có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng với bài viết này, các em đã có thể giải thành công các bài tập trong mục 1 trang 115, 116 SGK Toán 11 tập 1. Chúc các em học tốt!