Bài 8.28 trang 79 SGK Toán 11 tập 2 thuộc chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài tập này đòi hỏi học sinh phải nắm vững kiến thức về các công thức đạo hàm cơ bản và cách áp dụng chúng để giải quyết các bài toán cụ thể.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 8.28 trang 79 SGK Toán 11 tập 2, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Để chuẩn bị cho một buổi triển lãm quốc tế, các trang sức có giá trị lớn được đặt bảo mật trong các khối chóp từ giác như hình 867
Đề bài
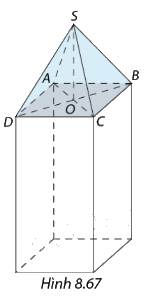
Để chuẩn bị cho một buổi triển lãm quốc tế, các trang sức có giá trị lớn được đặt bảo mật trong các khối chóp từ giác như hình 867 và đặt trên phía trên một trụ hình hộp chữ nhật có độ cao 1 m, đây là hình vuông cạnh 50 cm. Ban tổ chức sự kiện dự định dùng các tấm kính cường lực hình tam giác còn có cạnh bên là 60 cm để ráp lại thành khối chóp nói trên. Tỉnh khoảng cách tử đỉnh hình chóp đến mặt sàn nơi diễn ra buổi triển lãm.
Phương pháp giải - Xem chi tiết
Để tìm khoảng cách tử đỉnh hình chóp đến mặt sàn nơi diễn ra buổi triển lãm ta cần tìm độ dài SO.
Lời giải chi tiết
ABCD là hình vuông có cạnh 50 cm nên BD = \(50\sqrt 2 \). Suy ra DO = \(25\sqrt 2 \)
Khoảng cách từ đỉnh hình chóp đến mặt sàn là: \(100 + SO = 100 + \sqrt {S{D^2} - O{D^2}} = 100 + \sqrt {{{60}^2} - {{\left( {25\sqrt 2 } \right)}^2}} \approx 148\)
Bài 8.28 trang 79 SGK Toán 11 tập 2 thường yêu cầu học sinh thực hiện các thao tác như tính đạo hàm, tìm cực trị, và khảo sát hàm số. Để giải bài tập này một cách hiệu quả, cần tuân thủ các bước sau:
Ví dụ minh họa:
Giả sử hàm số cần khảo sát là f(x) = x3 - 3x2 + 2.
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | ↗ | ↘ | ↗ |
Từ bảng biến thiên, ta thấy hàm số đồng biến trên khoảng (-∞, 0) và (2, +∞), nghịch biến trên khoảng (0, 2). Điểm x = 0 là điểm cực đại, x = 2 là điểm cực tiểu.
Các dạng bài tập thường gặp:
Mẹo giải bài tập:
Tài liệu tham khảo:
Hy vọng với những hướng dẫn chi tiết trên, các em học sinh sẽ tự tin giải quyết Bài 8.28 trang 79 SGK Toán 11 tập 2 và các bài tập tương tự. Chúc các em học tập tốt!