Bài 5.10 trang 141 SGK Toán 11 tập 1 là một bài tập quan trọng trong chương trình học Toán 11. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu và phương pháp giải bài tập 5.10 trang 141 SGK Toán 11 tập 1, giúp các em học sinh nắm vững kiến thức và tự tin làm bài.
Lan tìm hiểu hàm lượng vitamin C trong một số loại rau củ quả và thống kê dữ liệu trong Bảng 5.26
Đề bài
Lan tìm hiểu hàm lượng vitamin C trong một số loại rau củ quả và thống kê dữ liệu trong Bảng 5.26 Lan muốn phân những loại rau củ mà mình tìm hiểu thành 4 nhóm tùy theo hàm lượng vitamin C của chúng: Nhóm I gồm khoảng 25% rau củ quả có hàm lượng vitamin C thấp ; nhóm II gồm 50% loại rau củ có hàm lượng vitamin C trung bình ; nhóm III gồm khoảng 25 % loại rau củ quả có hàm lượng vitamin C cao.
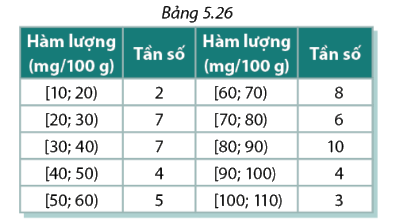
Hãy xác định:
a, Đầu mút phải khoảng biểu thị của hàm lượng vitamin C nhóm I
b, Đầu mút phải và đầu mút trái của hàm lượng vitamin C của nhóm II
c, Đầu mút trái khoảng biểu thị hàm lượng vitamin C của nhóm III
Phương pháp giải - Xem chi tiết
Sử dụng công thức tính tứ phân vị của mẫu số liệu
Lời giải chi tiết
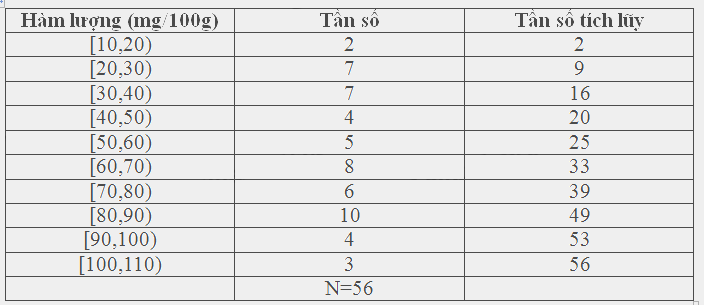
Ta có : \(\frac{N}{4} = \frac{{56}}{4} = 14 \Rightarrow \frac{N}{2} = 28 \Rightarrow \frac{{3N}}{4} = 42\)
Các nhóm chứa \({Q_1}\), \({Q_2}\) và \({Q_3}\) là [30,40); [60,70) và [80,90)
Độ dài các nhóm ghép đều là h= 10
Ta có: \({L_1} = 30,{n_1} = 7,{T_1} = 9\)\( \Rightarrow {Q_1} = {L_1} + \frac{{\frac{N}{4} - {T_1}}}{{{n_1}}}.h = 30 + \frac{{14 - 9}}{7}.10 \approx 37,14\)
\({L_2} = 60,{n_2} = 8,{T_2} = 25\)\( \Rightarrow {Q_2} = {L_2} + \frac{{\frac{N}{2} - {T_2}}}{{{n_2}}}.h = 60 + \frac{{28 - 25}}{8}.10 = 63,75\)
\({L_3} = 80,{n_3} = 10,{T_3} = 39\)\( \Rightarrow {Q_3} = {L_3} + \frac{{\frac{{3N}}{4} - {T_3}}}{{{n_3}}}.h = 80 + \frac{{42 - 39}}{{10}}.10 = 83\)
a, Đầu mút phải khoảng biểu thị của hàm lượng vitamin C nhóm I là \({Q_1} \approx 37,14\)
b, Đầu mút trái khoảng biểu thị của hàm lượng vitamin C nhóm II là \({Q_1} \approx 37,14\)
Đầu mút phải khoảng biểu thị của hàm lượng vitamin C nhóm II là \({Q_3} = 83\)
c, Đầu mút trái khoảng biểu thị hàm lượng vitamin C của nhóm III là \({Q_3} = 83\).
Bài 5.10 trang 141 SGK Toán 11 tập 1 thuộc chương trình Đại số, cụ thể là phần Đạo hàm. Bài toán này thường yêu cầu học sinh áp dụng các quy tắc tính đạo hàm của hàm số, đặc biệt là đạo hàm của hàm hợp và đạo hàm của hàm lượng giác.
Thông thường, bài 5.10 sẽ đưa ra một hàm số cụ thể và yêu cầu tính đạo hàm của hàm số đó tại một điểm cho trước hoặc tìm điều kiện để hàm số có đạo hàm. Đôi khi, bài toán còn yêu cầu sử dụng đạo hàm để giải các bài toán liên quan đến cực trị của hàm số.
Giả sử hàm số cần tính đạo hàm là: f(x) = sin(2x + 1). Để tính đạo hàm của hàm số này, ta sử dụng quy tắc đạo hàm của hàm hợp:
f'(x) = (sin(2x + 1))' = cos(2x + 1) * (2x + 1)' = 2cos(2x + 1)
Khi giải bài tập về đạo hàm, cần chú ý các điểm sau:
Đạo hàm có rất nhiều ứng dụng trong thực tế, bao gồm:
Hy vọng với lời giải chi tiết và phương pháp giải bài tập 5.10 trang 141 SGK Toán 11 tập 1, các em học sinh sẽ hiểu rõ hơn về đạo hàm và tự tin làm bài tập. Hãy truy cập giaitoan.edu.vn để xem thêm nhiều bài giải Toán 11 khác.