Bài 8.19 trang 72 SGK Toán 11 tập 2 thuộc chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài tập này đòi hỏi học sinh phải nắm vững kiến thức về các công thức đạo hàm cơ bản và cách áp dụng chúng vào giải quyết các bài toán cụ thể.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu cho Bài 8.19 trang 72 SGK Toán 11 tập 2, giúp học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hình chóp cụt tứ giác đều ABCD.A’B’C’D’, cạnh đáy lớn bằng \(5\sqrt 2 a\)
Đề bài
Cho hình chóp cụt tứ giác đều ABCD.A’B’C’D’, cạnh đáy lớn bằng \(5\sqrt 2 a\), cạnh đáy nhỏ bằng \(2\sqrt 2 a\) và chiều cao bằng 4a. Tỉnh độ dài cạnh bên của hình chóp cụt đều này.
Phương pháp giải - Xem chi tiết
Kẻ D’H, C’G vuông góc với CD. Tính DH. Áp dụng Py-ta-go để tính DD’.
Lời giải chi tiết
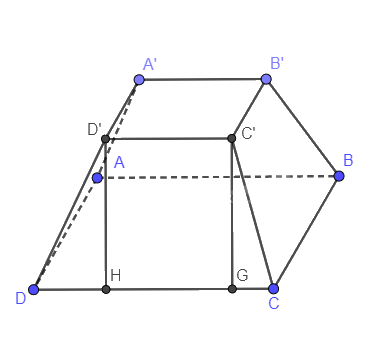
Kẻ D’H, C’G vuông góc với CD nên D’H song song với C’G
Mà C’D’ song song với HG
Suy ra D’C’GH là hình chữ nhật nên HG = \(2\sqrt 2 a\)
\( \Rightarrow DH + CG = 3\sqrt 2 a \Rightarrow DH = CG = \frac{{3\sqrt 2 }}{2}a\)
Xét tam giác D’HD vuông tại H có:
\(DD' = \sqrt {D'{H^2} + D{H^2}} = \sqrt {{{\left( {4a} \right)}^2} + {{\left( {\frac{{3\sqrt 2 }}{2}a} \right)}^2}} = \frac{{41}}{2}a\)
Bài 8.19 trang 72 SGK Toán 11 tập 2 yêu cầu học sinh giải một bài toán cụ thể liên quan đến việc tìm đạo hàm và ứng dụng đạo hàm để giải quyết một vấn đề thực tế. Để giải bài toán này, học sinh cần thực hiện các bước sau:
Giả sử bài toán yêu cầu tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = x3 - 3x2 + 2 trên đoạn [-1; 3].
Khi giải các bài tập về đạo hàm và ứng dụng của đạo hàm, học sinh cần chú ý các điểm sau:
Để hiểu sâu hơn về đạo hàm và ứng dụng của đạo hàm, học sinh có thể tìm hiểu thêm về các khái niệm liên quan như giới hạn, liên tục, đạo hàm riêng, tích phân. Việc nắm vững các kiến thức này sẽ giúp học sinh giải quyết các bài toán phức tạp hơn và ứng dụng toán học vào thực tế.
Bài 8.19 trang 72 SGK Toán 11 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Hy vọng với lời giải chi tiết và các hướng dẫn trên, học sinh sẽ hiểu rõ phương pháp giải và tự tin làm bài tập.
Giaitoan.edu.vn luôn đồng hành cùng học sinh trên con đường chinh phục môn Toán. Chúc các em học tập tốt!