Bài 8.21 trang 79 SGK Toán 11 tập 2 thuộc chương trình học Toán 11, tập trung vào việc giải các bài toán liên quan đến phép đếm và các quy tắc tổ hợp. Bài tập này giúp học sinh rèn luyện kỹ năng áp dụng công thức và tư duy logic để giải quyết các vấn đề thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 8.21 trang 79, giúp bạn hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hình chóp tam giác đều S.ABC có cạnh bên bằng 4a và cạnh đáy bằng 6a. Tính khoảng cách từ S đến mặt phẳng (ABC).
Đề bài
Cho hình chóp tam giác đều S.ABC có cạnh bên bằng 4a và cạnh đáy bằng 6a. Tính khoảng cách từ S đến mặt phẳng (ABC).
Phương pháp giải - Xem chi tiết
Tìm khoảng cách giữa M và (P):
+ Tìm (Q) chứa M và vuông góc với (P) theo giao tuyến d.
+ Từ M hạ MH vuông góc với d (H thuộc d).
+ Khi đó MH là khoảng cách cần tìm.
Lời giải chi tiết
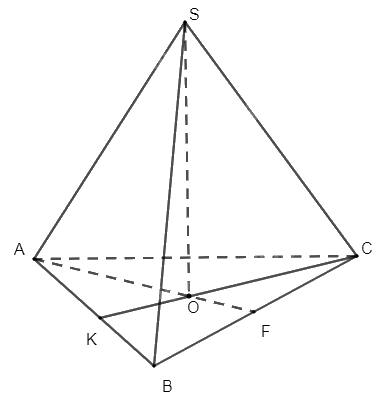
Gọi O là trọng tâm tam giác ABC
Ta có: BC \(\bot\) AF, BC \(\bot\) SF
\(\Rightarrow\) BC \(\bot\) (SAF). Do đó, BC \(\bot\) SO (1)
Tương tự, AB \(\bot\) (SCK). Suy ra, AB \(\bot\) SO (2)
Từ (1) và(2), SO \(\bot\) (ABC)
Vậy d(S,(ABC)) = SO
\(\begin{array}{l}AH = 3\sqrt 3 a\\AO = \frac{2}{3}AH = 2\sqrt 3 \\SO = \sqrt {S{A^2} - A{O^2}} = 2a\end{array}\)
Bài 8.21 trang 79 SGK Toán 11 tập 2 yêu cầu chúng ta giải một bài toán về tổ hợp. Để giải bài toán này, chúng ta cần nắm vững các khái niệm cơ bản về hoán vị, chỉnh hợp và tổ hợp.
Trước khi đi vào giải chi tiết, chúng ta cần phân tích kỹ đề bài để xác định rõ yêu cầu và các dữ kiện đã cho. Bài toán thường yêu cầu tính số lượng các cách sắp xếp, chọn lựa hoặc phân chia các đối tượng theo một quy tắc nhất định.
(Nội dung lời giải chi tiết sẽ được trình bày tại đây, bao gồm các bước giải, giải thích rõ ràng và ví dụ minh họa. Lời giải sẽ được trình bày theo từng bước để người học dễ dàng theo dõi và hiểu được phương pháp giải.)
Ví dụ, nếu bài toán yêu cầu tính số cách chọn 3 học sinh từ một lớp 20 học sinh để thành lập một tổ, ta sẽ sử dụng công thức tổ hợp: C203 = 20! / (3! * 17!) = (20 * 19 * 18) / (3 * 2 * 1) = 1140.
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập về tổ hợp, bạn có thể tham khảo các bài tập tương tự sau:
Ngoài các công thức cơ bản về hoán vị, chỉnh hợp và tổ hợp, bạn cũng nên tìm hiểu thêm về các ứng dụng của chúng trong thực tế, chẳng hạn như trong lĩnh vực thống kê, xác suất và khoa học máy tính.
| Công thức | Mô tả |
|---|---|
| Pn = n! | Hoán vị của n phần tử |
| Ank = n! / (n-k)! | Chỉnh hợp chập k của n phần tử |
| Cnk = n! / (k! * (n-k)!) | Tổ hợp chập k của n phần tử |
Hy vọng với lời giải chi tiết và hướng dẫn này, bạn sẽ hiểu rõ hơn về Bài 8.21 trang 79 SGK Toán 11 tập 2 và có thể tự tin giải các bài tập tương tự. Hãy luyện tập thường xuyên để nắm vững kiến thức và đạt kết quả tốt trong môn Toán.