Bài 8.45 trang 90 SGK Toán 11 tập 2 thuộc chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến đường thẳng và mặt phẳng trong không gian. Bài tập này đòi hỏi học sinh phải nắm vững kiến thức về vectơ, phương trình đường thẳng và mặt phẳng.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh hiểu rõ phương pháp giải và tự tin làm bài tập. Chúng tôi luôn cập nhật đáp án chính xác và nhanh chóng.
Cho tử diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = OB = OC.
Đề bài
Cho tử diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = OB = OC. Gọi M là trung điểm của BC. Góc giữa hai đường thẳng OM và AB bằng
A. 900.
B. 300.
C. 600.
D. 450.
Phương pháp giải - Xem chi tiết
Chọn 2 đường thẳng cắt nhau c và d lần lượt song song với a và b. Khi đó góc giữa c và d là góc giữa a và b.
Lời giải chi tiết
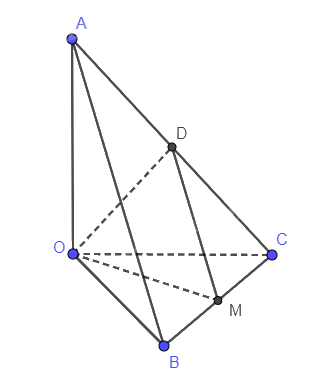
Đặt OA = OB = OC = a
Gọi D là trung điểm của AC nên DM // AB và bằng một nửa AB
\( \Rightarrow \widehat {\left( {OM,AB} \right)} = \widehat {\left( {OM,DM} \right)} = \widehat {OMD}\)
Ta có: OA vuông góc và bằng OC nên tam giác OAC là tam giác vuông cân tại C
\(AC = \sqrt {O{A^2} + O{B^2}} = \sqrt 2 a\)
\(\begin{array}{l}AC.OD = OA.OC\\ \Leftrightarrow OD = \frac{{\sqrt 2 }}{2}a\end{array}\)
Tương tự với OM, ta có: \(OM = \frac{{\sqrt 2 }}{2}a\)
\(AB = \sqrt {O{A^2} + O{B^2}} = \sqrt 2 a\)
Suy ra \(DM = \frac{{\sqrt 2 }}{2}a\)
Vậy tam giác DOM đều. Suy ra \(\widehat {OMD} = {60^0}\).
Chọn đáp án C.
Bài 8.45 trang 90 SGK Toán 11 tập 2 yêu cầu giải một bài toán về vị trí tương đối giữa đường thẳng và mặt phẳng trong không gian. Để giải bài toán này, chúng ta cần nắm vững các kiến thức sau:
Phân tích bài toán:
Trước khi bắt tay vào giải, chúng ta cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho (phương trình đường thẳng, phương trình mặt phẳng) và yêu cầu của bài toán (xác định vị trí tương đối, tìm giao điểm, tính khoảng cách,...). Sau đó, chúng ta sẽ áp dụng các kiến thức đã học để giải quyết bài toán.
Lời giải chi tiết:
(Ở đây sẽ là lời giải chi tiết của bài toán Bài 8.45 trang 90 SGK Toán 11 tập 2. Lời giải sẽ bao gồm các bước giải cụ thể, giải thích rõ ràng từng bước và kết luận cuối cùng. Lời giải sẽ được trình bày một cách logic và dễ hiểu, giúp học sinh nắm vững phương pháp giải.)
Ví dụ minh họa:
Để giúp học sinh hiểu rõ hơn về cách giải bài toán này, chúng ta sẽ xét một ví dụ minh họa cụ thể. Ví dụ này sẽ có cấu trúc tương tự như Bài 8.45 trang 90 SGK Toán 11 tập 2, nhưng có các số liệu khác nhau. Chúng ta sẽ giải ví dụ này theo các bước tương tự như lời giải chi tiết ở trên.
Lưu ý quan trọng:
Bài tập tương tự:
Để rèn luyện kỹ năng giải bài toán về vị trí tương đối giữa đường thẳng và mặt phẳng, chúng ta có thể làm thêm một số bài tập tương tự. Các bài tập này có thể được tìm thấy trong SGK Toán 11 tập 2, sách bài tập Toán 11 hoặc trên các trang web học toán online.
Tổng kết:
Bài 8.45 trang 90 SGK Toán 11 tập 2 là một bài toán quan trọng trong chương trình học Toán 11. Việc nắm vững kiến thức và phương pháp giải bài toán này sẽ giúp học sinh tự tin làm bài kiểm tra và thi cử. Giaitoan.edu.vn hy vọng rằng lời giải chi tiết và các ví dụ minh họa ở trên sẽ giúp học sinh hiểu rõ hơn về bài toán này.
Các chủ đề liên quan:
Tài liệu tham khảo: