Chào mừng bạn đến với bài học về Lý thuyết Lũy thừa trong chương trình SGK Toán 11. Đây là một phần kiến thức quan trọng, đặt nền móng cho các chương trình học toán nâng cao hơn. Bài viết này sẽ cung cấp cho bạn một cái nhìn tổng quan và chi tiết về các khái niệm, tính chất và ứng dụng của lũy thừa.
Giaitoan.edu.vn cam kết mang đến cho bạn những bài giảng dễ hiểu, bài tập đa dạng và phương pháp học tập hiệu quả nhất để bạn có thể tự tin chinh phục môn Toán.
A. Lý thuyết 1. Lũy thừa với số mũ nguyên
A. Lý thuyết
1. Lũy thừa với số mũ nguyên
Cho n là một số nguyên dương. - Với a là số thực tùy ý, lũy thừa bậc n của a là tích của n thừa số a. \({a^n} = a.a...a\) (n thừa số a). - Với \(a \ne 0\): \({a^{ - n}} = \frac{1}{{{a^n}}}\). |
Trong biểu thức \({a^n}\), ta gọi a là cơ số, số nguyên n là số mũ.
Lưu ý:
- Với \(a \ne 0\) thì \({a^0} = 1\).
- \({0^0}\) với \({0^{ - n}}\) với \(n \in \mathbb{N}\) không có nghĩa.
Cho a, b là các số thực khác 0 và với các số nguyên m, n, ta có: +) \({a^m}.{a^n} = {a^{m + n}}\) +) \(\frac{{{a^m}}}{{{a^n}}} = {a^{m - n}}\) +) \({({a^m})^n} = {a^{m.n}}\) +) \({(a.b)^m} = {a^m}.{b^m}\) +) \({\left( {\frac{a}{b}} \right)^m} = \frac{{{a^m}}}{{{b^m}}}\) |
2. Lúy thừa với số mũ hữu tỉ
| Cho số thực b và số nguyên dương n \((n \ge 2)\). Số a được gọi là căn bậc n của số b nếu \({a^n} = b\). |
Lưu ý:
- Với n lẻ và \(b \in \mathbb{R}\), có duy nhất một căn bậc n của b, kí hiệu là \(\sqrt[n]{b}\).
- Với n chẵn và:
+ b < 0: Không tồn tại căn bậc n của b.
+ b = 0: Có một căn bậc n của b là số 0.
+ b > 0: Có hai căn bậc n trái dấu, giá trị dương kí hiệu là \(\sqrt[n]{b}\) và giá trị âm kí hiệu là \( - \sqrt[n]{b}\).
Cho số thực a dương và số hữu tỉ \(r = \frac{m}{n}\), trong đó \(m \in \mathbb{Z}\), \(n \in \mathbb{N}\), \(n \ge 2\). Lũy thừa của số a với số mũ r, kí hiệu \({a^r}\) xác định bởi: \({a^r} = {a^{\frac{m}{n}}} = \sqrt[n]{{{a^m}}}\). |
Lưu ý : \({a^{\frac{1}{n}}} = \sqrt[n]{a}\) với a > 0 và \(n \in \mathbb{N}\), \(n \ge 2\).
| Lũy thừa với số mũ hữu tỉ của số thực dương có đầy đủ các tính chất như lũy thừa với số mũ nguyên. |
3. Lũy thừa với số mũ thực
Cho số thực a dương và số vô tỉ \(\alpha \), trong đó \(\alpha = \mathop {\lim }\limits_{x \to + \infty } {r_n}\) với \(({r_n})\) là một dãy số hữu tỉ. Giới hạn của dãy số \(({a^{{r_n}}})\) gọi là lũy thừa của số a với số mũ \(\alpha \), kí hiệu \({a^\alpha }\). \({a^\alpha } = \mathop {\lim }\limits_{x \to + \infty } {a^{{r_n}}}\) với \(\alpha = \mathop {\lim }\limits_{x \to + \infty } {r_n}\). |
Lưu ý:
- Từ định nghĩa, ta có \({1^\alpha } = 1\) \((\alpha \in \mathbb{R})\).
- Khi xét lũy thừa với số mũ 0 và số mũ nguyên âm thì cơ số khác 0.
- Khi xét lũy thừa với số mũ không nguyên thì cơ số phải dương.
| Lũy thừa với số mũ thực dương có các tính chất tương tự lũy thừa vơi số mũ nguyên. |
B. Bài tập
Bài 1:
a) Không dùng máy tính cầm tay, rút gọn giá trị biểu thức:
\(A = {\left( {\frac{1}{3}} \right)^{ - 10}}{.27^{ - 3}} + {(0,2)^{ - 4}}{.25^{ - 2}}{.128^{ - 1}}.{\left( {\frac{1}{2}} \right)^{ - 9}}\).
b) Rút gọn biểu thức: \(B = \left[ {\frac{{a\sqrt 2 }}{{{{(1 + {a^2})}^{ - 1}}}} - \frac{{2\sqrt 2 }}{{{a^{ - 1}}}}} \right].\frac{{{a^{ - 1}}}}{{1 - {a^{ - 2}}}}\) \((a \ne 0,a \ne 1,a \ne - 1)\).
Giải:
a) \(A = {({3^{ - 1}})^{ - 10}}.{({3^3})^{ - 3}} + {({5^{ - 1}})^{ - 4}}.{({5^2})^{ - 2}} + {({2^7})^{ - 1}}.{({2^{ - 1}})^{ - 9}}\)
\( = {3^{10}}{.3^{ - 9}} + {5^4}{.5^{ - 4}} + {2^{ - 7}}{.2^9}\)
\( = {3^1} + {5^0} + {2^2} = 8\).
b) \(B = \left[ {a\sqrt 2 (1 + {a^2}) - 2\sqrt 2 a} \right].\frac{1}{{{a^3}(1 - {a^{ - 2}})}}\)
\( = (a\sqrt 2 + {a^3}\sqrt 2 - 2a\sqrt 2 ).\frac{1}{{{a^3} - a}}\)
\( = a\sqrt 2 ({a^2} - 1).\frac{1}{{a({a^2} - 1)}} = \sqrt 2 \).
Bài 2:
a) Không dùng máy tính cầm tay, tính giá trị biểu thức \(A = {\left( {\frac{1}{{27}}} \right)^{\frac{1}{3}}} + {9^{ - \frac{3}{2}}}\).
b) Rút gọn biểu thức \(C = \frac{{{x^{\frac{6}{5}}}y + x{y^{\frac{6}{5}}}}}{{\sqrt[5]{x} + \sqrt[5]{y}}}\) (x > 0, y > 0).
Giải:
a) Ta có \({\left( {\frac{1}{{27}}} \right)^{\frac{1}{3}}} = \sqrt[3]{{\frac{1}{{27}}}} = \frac{1}{3}\); \({9^{ - \frac{3}{2}}} = \sqrt {{9^{ - 3}}} = \sqrt {\frac{1}{{{9^3}}}} = {\left( {\sqrt {\frac{1}{9}} } \right)^3} = \frac{1}{{27}}\).
Vậy \(A = {\left( {\frac{1}{{27}}} \right)^{\frac{1}{3}}} + {9^{ - \frac{3}{2}}} = \frac{1}{3} + \frac{1}{{27}} = \frac{{10}}{{27}}\).
b) Với x, y là các số dương, theo định nghĩa, ta có \(C = \frac{{xy\left( {{x^{\frac{1}{5}}} + {y^{\frac{1}{5}}}} \right)}}{{{x^{\frac{1}{5}}} + {y^{\frac{1}{5}}}}} = xy\).
Bài 3: Rút gọn biểu thức \(E = \frac{{{a^{\sqrt 5 + 1}}.{a^{2 - \sqrt 5 }}}}{{{{({a^{\sqrt 7 - 3}})}^{\sqrt 7 + 3}}}}\) (a > 0).
Giải:
\(E = \frac{{{a^{\sqrt 5 + 1 + 2 - \sqrt 5 }}}}{{{a^{(\sqrt 7 - 3)(}}^{\sqrt 7 + 3)}}} = \frac{{{a^3}}}{{{a^{ - 2}}}} = {a^5}\).
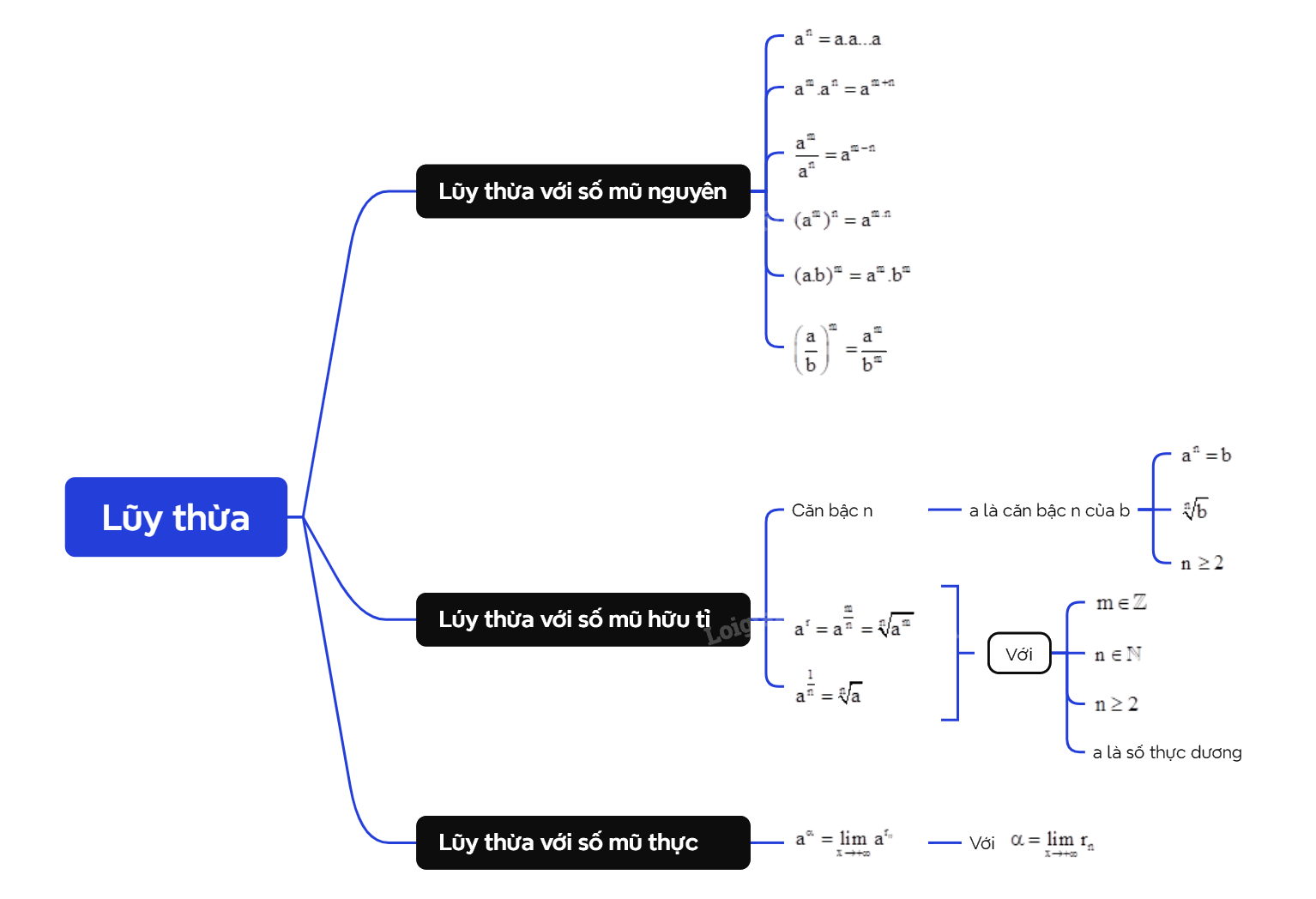
Lũy thừa là một phép toán cơ bản trong toán học, biểu thị việc một số (cơ số) được nhân với chính nó một số lần nhất định (số mũ). Trong chương trình Toán 11, việc nắm vững lý thuyết lũy thừa là vô cùng quan trọng, không chỉ để giải các bài tập trong SGK mà còn là nền tảng cho việc học các kiến thức toán học phức tạp hơn như hàm số mũ, logarit và các ứng dụng trong thực tế.
Với a là một số thực và n là một số nguyên dương, lũy thừa bậc n của a, ký hiệu là an, là tích của n thừa số bằng a:
an = a × a × ... × a (n thừa số)
Trong đó:
Việc hiểu rõ các tính chất của lũy thừa giúp chúng ta đơn giản hóa các biểu thức toán học và giải quyết các bài toán một cách hiệu quả hơn. Dưới đây là một số tính chất quan trọng:
Khi số mũ là một số nguyên âm, chúng ta cần lưu ý đến định nghĩa và các tính chất liên quan. Ví dụ:
2-3 = 1 / 23 = 1 / 8
Trong chương trình Toán 11, chúng ta sẽ tìm hiểu sâu hơn về lũy thừa với số mũ phân số và mối liên hệ giữa lũy thừa và căn bậc n. Định nghĩa:
am/n = n√am (với a > 0)
Để củng cố kiến thức về lý thuyết lũy thừa, chúng ta hãy cùng giải một số bài tập ví dụ:
Rút gọn biểu thức: (23 × 32)2
Giải:
(23 × 32)2 = (23)2 × (32)2 = 26 × 34 = 64 × 81 = 5184
Tính giá trị của biểu thức: (5-2 × 23) / 4-1
Giải:
(5-2 × 23) / 4-1 = (1/25 × 8) / (1/4) = (8/25) × 4 = 32/25
Lũy thừa có rất nhiều ứng dụng trong thực tế, từ khoa học, kỹ thuật đến kinh tế và tài chính. Ví dụ:
Lý thuyết lũy thừa là một phần kiến thức quan trọng trong chương trình Toán 11. Việc nắm vững các định nghĩa, tính chất và ứng dụng của lũy thừa sẽ giúp bạn giải quyết các bài toán một cách hiệu quả và tự tin hơn. Hãy luyện tập thường xuyên và áp dụng kiến thức vào thực tế để đạt được kết quả tốt nhất.