Bài 8.29 trang 83 SGK Toán 11 tập 2 là một bài tập quan trọng trong chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng giải bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững phương pháp giải và tự tin làm bài tập.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông có AC = 2a.
Đề bài
Cho hình chóp S.ABCD có đáy ABCD là hình vuông có AC = 2a. Hình chiếu vuông góc của S trên mặt phẳng (ABCD) là trung điểm H của cạnh AB và tam giác SAB vuông tại S. Tính thể tích khối chóp này.
Phương pháp giải - Xem chi tiết
Công thức tính thể tích hình chóp: \(V = \frac{1}{3}S.h\) với S là diện tích đáy, h là đường cao.
Hệ thức lượng trong tam giác ABC vuông tại A có AH là đường cao: \(AB.AC = AH.BC\)
Lời giải chi tiết
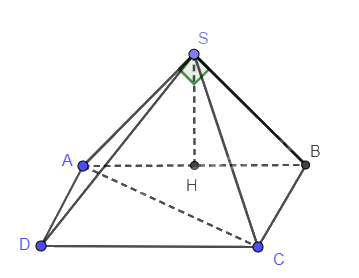
Ta có:
\(\begin{array}{l}AC = \sqrt {A{B^2} + C{B^2}} \\ \Leftrightarrow 2a = \sqrt {2A{B^2}} \\ \Leftrightarrow 4{a^2} = 2A{B^2}\\ \Leftrightarrow A{B^2} = 2{a^2}\\ \Leftrightarrow AB = \sqrt 2 a\end{array}\)
Xét tam giác SAB vuông tại S:
\(\begin{array}{l}AB = \sqrt {S{A^2} + S{B^2}} \\ \Leftrightarrow \sqrt 2 a = \sqrt {2S{A^2}} \\ \Leftrightarrow 2{a^2} = 2S{A^2}\\ \Leftrightarrow SA = a\end{array}\)
Tam giác vuông SAB có SH là đường cao có:
\(\begin{array}{l}SH.AB = SA.SB\\ \Leftrightarrow SH = \frac{{a.a}}{{\sqrt 2 a}} = \frac{{\sqrt 2 }}{a}a\end{array}\)
\(V = \frac{1}{3}S.h = \frac{1}{3}.A{B^2}.SH = \frac{1}{3}.{\left( {\sqrt 2 a} \right)^2}.\frac{{\sqrt 2 }}{2}a = \frac{{\sqrt 2 }}{3}{a^3}\)
Bài 8.29 thuộc chương trình giải tích lớp 11, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài toán này thường yêu cầu học sinh xác định các điểm cực trị của hàm số, khoảng đồng biến, nghịch biến và vẽ đồ thị hàm số.
Bài 8.29 thường có dạng như sau: Cho hàm số y = f(x). Hãy tìm:
Tập xác định của hàm số.
Các điểm cực trị của hàm số.
Khoảng đồng biến, nghịch biến của hàm số.
Giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng cho trước.
Để giải bài 8.29, học sinh cần thực hiện các bước sau:
Tính đạo hàm f'(x): Đây là bước quan trọng nhất để xác định các điểm cực trị và khoảng đồng biến, nghịch biến của hàm số.
Tìm các điểm cực trị: Giải phương trình f'(x) = 0 để tìm các điểm nghiệm. Sau đó, xét dấu của f'(x) để xác định loại điểm cực trị (cực đại hoặc cực tiểu).
Xác định khoảng đồng biến, nghịch biến: Dựa vào dấu của f'(x) để xác định khoảng đồng biến (f'(x) > 0) và khoảng nghịch biến (f'(x) < 0).
Tìm giá trị lớn nhất, giá trị nhỏ nhất: Xét giá trị của hàm số tại các điểm cực trị và tại các đầu mút của khoảng cho trước để tìm giá trị lớn nhất và giá trị nhỏ nhất.
Giả sử cho hàm số y = x3 - 3x2 + 2.
Bước 1: Tính đạo hàm
y' = 3x2 - 6x
Bước 2: Tìm các điểm cực trị
Giải phương trình y' = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy x = 0 hoặc x = 2
Xét dấu của y':
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + |
Vậy hàm số đạt cực đại tại x = 0 và cực tiểu tại x = 2.
Bước 3: Xác định khoảng đồng biến, nghịch biến
Hàm số đồng biến trên khoảng (-∞, 0) và (2, +∞).
Hàm số nghịch biến trên khoảng (0, 2).
Bước 4: Tìm giá trị lớn nhất, giá trị nhỏ nhất
Giá trị cực đại tại x = 0 là y = 2.
Giá trị cực tiểu tại x = 2 là y = -2.
Luôn kiểm tra tập xác định của hàm số trước khi tính đạo hàm.
Sử dụng các quy tắc đạo hàm một cách chính xác.
Xét dấu đạo hàm một cách cẩn thận để xác định khoảng đồng biến, nghịch biến và các điểm cực trị.
Vẽ đồ thị hàm số để kiểm tra lại kết quả.
Bài 8.29 trang 83 SGK Toán 11 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Việc nắm vững phương pháp giải bài tập này sẽ giúp học sinh tự tin hơn trong các kỳ thi và trong quá trình học tập.
Tại giaitoan.edu.vn, chúng tôi luôn cập nhật những lời giải chi tiết, dễ hiểu và các bài tập tương tự để giúp học sinh học tập hiệu quả nhất.