Chào mừng bạn đến với bài học về lý thuyết các quy tắc tính đạo hàm trong chương trình Toán 11. Đây là một phần kiến thức quan trọng, nền tảng cho việc giải quyết các bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm trong các lĩnh vực khác.
Tại giaitoan.edu.vn, chúng tôi cung cấp tài liệu học tập đầy đủ, chi tiết và dễ hiểu, giúp bạn nắm vững kiến thức một cách nhanh chóng và hiệu quả.
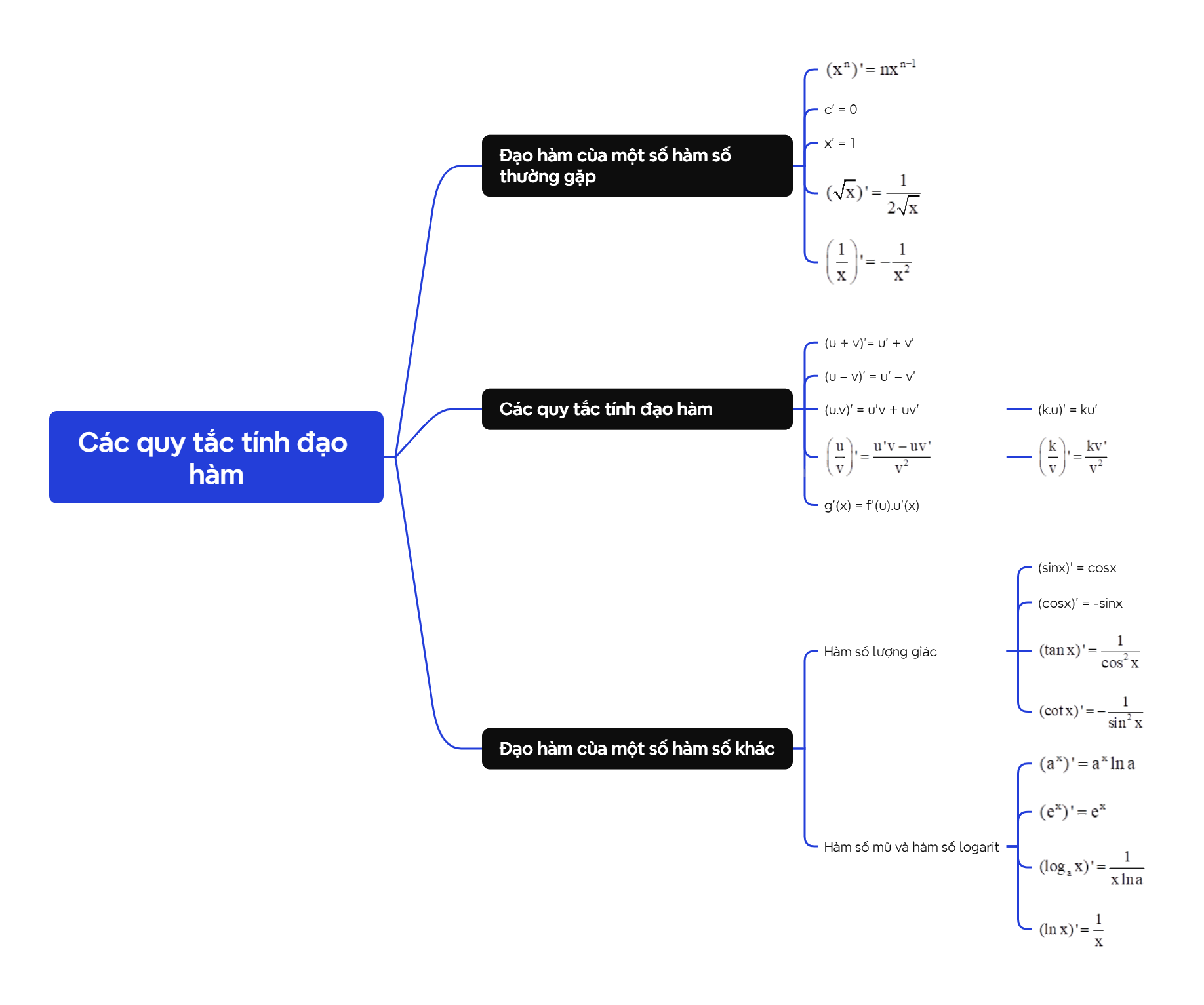
A. Lý thuyết 1. Đạo hàm của một số hàm số thường gặp
A. Lý thuyết
1. Đạo hàm của một số hàm số thường gặp
| Hàm số \(y = {x^n}\) \((n \in {\mathbb{N}^*})\) có đạo hàm tại mọi \(x \in \mathbb{R}\) và \(({x^n})' = n{x^{n - 1}}\). |
Ghi chú:
+ c’ = 0.
+ x’ = 1.
+ \((\sqrt x )' = \frac{1}{{2\sqrt x }}\) \((x \ne 0)\).
+ \(\left( {\frac{1}{x}} \right)' = - \frac{1}{{{x^2}}}\) \((x \ne 0)\).
2. Các quy tắc tính đạo hàm
a) Đạo hàm của tổng, hiệu hai hàm số
Nếu hai hàm số u = u(x) và v = v(x) có đạo hàm trên khoảng (a;b) thì (u + v)’= u’ + v’; (u – v)’ = u’ – v’. |
b) Đạo hàm của tích, thương hai hàm số
Nếu hai hàm số u = u(x) và v = v(x) có đạo hàm trên khoảng xác định thì (u.v)’ = u’v + uv’; \(\left( {\frac{u}{v}} \right)' = \frac{{u'v - uv'}}{{{v^2}}}\) \((v = v(x) \ne 0)\). |
Lưu ý:
+ (k.u)’ = ku’ với \(k \in \mathbb{R}\).
+ \(\left( {\frac{k}{v}} \right)' = \frac{{kv'}}{{{v^2}}}\) với \(k \in \mathbb{R}\).
c) Đạo hàm của hàm hợp
* Hàm hợp
Cho hai hàm số f(u) và u = u(x). Hàm số y = f(u(x)) được gọi là hàm số hợp của hai hàm số f(u) và u(x).
* Đạo hàm của hàm hợp
Nếu hàm số u = u(x) có đạo hàm tại x là u’(x) và u = f(u) có đạo hàm tại u là f’(u) thì hàm hợp g(x) = f(u(x)) có đạo hàm tại x là g’(x) = f’(u).u’(x). |
3. Đạo hàm của một số hàm số khác
a) Đạo hàm của hàm số lượng giác
+ (sinx)’ = cosx + (cosx)’ = -sinx + \((\tan x)' = \frac{1}{{{{\cos }^2}x}}\), \(x \ne \frac{\pi }{2} + k\pi \) \((k \in \mathbb{Z})\) + \((\cot x)' = - \frac{1}{{{{\sin }^2}x}}\), \(x \ne k\pi \) \((k \in \mathbb{Z})\) |
b) Đạo hàm của hàm số mũ và hàm số logarit
Cho a > 0, \(a \ne 1\). + \(({a^x})' = {a^x}\ln a\) + \(({e^x})' = {e^x}\), \(x \in \mathbb{R}\) + \(({\log _a}x)' = \frac{1}{{x\ln a}}\), x > 0 + \((\ln x)' = \frac{1}{x}\), x > 0 |
B. Bài tập
Bài 1: Tính đạo hàm của hàm số \(y = {x^5} - {x^3} + x - 10\).
Giải:
\(y' = \left( {{x^5}} \right)' - \left( {{x^3}} \right)' + \left( x \right)' - \left( {10} \right)' = 5{x^4} - 3{x^2} + 1\).
Bài 2: Tính đạo hàm của các hàm số sau:
a) \(y = 4{x^2} - \frac{{\sqrt x }}{2} + \frac{5}{x}\).
b) \(y = (2{x^3} + 1)(\sqrt x - 3)\).
c) \(y = \frac{{2x - 1}}{{x + 1}}\).
Giải:
a) Với x > 0, ta có \(y = 4\left( {{x^2}} \right)' - \frac{1}{2}\left( {\sqrt x } \right)' + 5\left( {\frac{1}{x}} \right)' = 8x - \frac{1}{{4\sqrt x }} - \frac{5}{{{x^2}}}\).
b) Với x > 0, ta có \(y' = (2{x^3} + 1)'(\sqrt x - 3) + (2{x^3} + 1)(\sqrt x - 3)' = 6{x^2}(\sqrt x - 3) + (2{x^3} + 1)\frac{1}{{2\sqrt x }}\).
c) Với \(x \ne - 1\), ta có \(y' = \frac{{\left( {2x - 1} \right)'\left( {x + 1} \right) - \left( {2x - 1} \right)\left( {x + 1} \right)'}}{{{{\left( {x + 1} \right)}^2}}} = \frac{{2(x + 1) - (2x - 1)}}{{{{\left( {x + 1} \right)}^2}}} = \frac{3}{{{{\left( {x + 1} \right)}^2}}}\).
Bài 3: Tính đạo hàm của các hàm số sau:
a) \(y = {({x^2} + x)^8}\).
b) \(y = \frac{1}{{\sqrt x + 1}}\).
Giải:
a) \(y = \left[ {{{({x^2} + x)}^8}} \right]' = ({x^2} + x)'.8{({x^2} + x)^{8 - 1}} = 8(2x + 1){({x^2} + x)^7}\).
b) \(y' = \left( {\frac{1}{{\sqrt x + 1}}} \right)' = \frac{{\left( {\sqrt x + 1} \right)'}}{{{{\left( {\sqrt x + 1} \right)}^2}}} = \frac{1}{{{{\left( {\sqrt x + 1} \right)}^2}}}.\frac{1}{{2\sqrt x }}\).
Bài 4: Tính đạo hàm của các hàm số sau:
a) \(y = 2\sin x - 3\cos x\).
b) \(y = x\tan x\).
c) \(y = \sin \left( {2x - \frac{\pi }{6}} \right)\).
d) \(y = {\cos ^3}3x\).
Giải:
a) \(y' = 2\left( {\sin x} \right)' - 3\left( {\cos x} \right)' = 2\cos x + 3\sin x\).
b) Với \(x \ne \frac{\pi }{2} + k\pi \) \((k \in \mathbb{Z})\), ta có \(y = x'.\tan x + x.(\tan x)' = \tan x + \frac{x}{{{{\cos }^2}x}}\).
c) \(y = \sin \left( {2x - \frac{\pi }{6}} \right)\).
d) \(y' = 3{\cos ^2}3x.(\cos 3x)' = - 3{\cos ^2}3x.(3x)'.\sin 3x = - 9{\cos ^2}3x.\sin 3x\).
Bài 5: Tính đạo hàm của các hàm số sau:
a) \(y = {3^{2{x^2} - x}}\).
b) \(y = {\log _2}({x^2} + 2x + 3)\).
c) \(y = x{e^x}\).
Giải:
a) \(y' = (2{x^2} - x)'{.3^{2{x^2} - x}}.\ln 3 = (4x - 1){.3^{2{x^2} - x}}.\ln 3\).
b) \(y' = \frac{{({x^2} + 2x + 3)'}}{{({x^2} + 2x + 3)\ln 2}} = \frac{{2x + 2}}{{({x^2} + 2x + 3)\ln 2}}\).
c) \(y' = (x)'{e^x} + x({e^x})' = {e^x} + x{e^x}\).
Đạo hàm là một khái niệm cơ bản trong giải tích, đóng vai trò quan trọng trong việc nghiên cứu sự thay đổi của hàm số. Trong chương trình Toán 11, học sinh sẽ được làm quen với các quy tắc tính đạo hàm, giúp đơn giản hóa quá trình tìm đạo hàm của các hàm số phức tạp.
Trước khi đi vào các quy tắc, chúng ta cần nắm vững đạo hàm của một số hàm số cơ bản:
Nếu u và v là hai hàm số có đạo hàm, thì:
Quy tắc này cho phép chúng ta tính đạo hàm của một hàm số là tổng hoặc hiệu của nhiều hàm số đơn giản bằng cách tính đạo hàm của từng hàm số thành phần và cộng hoặc trừ chúng lại.
Nếu u và v là hai hàm số có đạo hàm, thì:
(uv)' = u'v + uv'
Quy tắc này được sử dụng để tính đạo hàm của tích của hai hàm số. Ví dụ, để tính đạo hàm của x2sin x, ta áp dụng quy tắc này với u = x2 và v = sin x.
Nếu u và v là hai hàm số có đạo hàm và v ≠ 0, thì:
(u/v)' = (u'v - uv')/v2
Quy tắc này được sử dụng để tính đạo hàm của thương của hai hàm số. Ví dụ, để tính đạo hàm của sin x / x, ta áp dụng quy tắc này với u = sin x và v = x.
Nếu y = f(u) và u = g(x), thì:
dy/dx = (dy/du) * (du/dx)
Quy tắc này được sử dụng để tính đạo hàm của hàm hợp, tức là hàm số được tạo thành bằng cách thay một hàm số vào một hàm số khác. Ví dụ, để tính đạo hàm của sin(x2), ta áp dụng quy tắc này với f(u) = sin u và g(x) = x2.
Ví dụ 1: Tính đạo hàm của hàm số f(x) = 3x2 + 2x - 1
Áp dụng quy tắc đạo hàm của tổng và hiệu, ta có:
f'(x) = (3x2)' + (2x)' - (1)' = 6x + 2 - 0 = 6x + 2
Ví dụ 2: Tính đạo hàm của hàm số g(x) = xsin x
Áp dụng quy tắc đạo hàm của tích, ta có:
g'(x) = (x)'sin x + x(sin x)' = 1 * sin x + x * cos x = sin x + xcos x
Để nắm vững các quy tắc tính đạo hàm, bạn cần luyện tập thường xuyên với các bài tập khác nhau. Hãy tìm các bài tập trong SGK Toán 11 và các tài liệu tham khảo khác để rèn luyện kỹ năng của mình.
Lý thuyết các quy tắc tính đạo hàm là một phần kiến thức quan trọng trong chương trình Toán 11. Việc nắm vững các quy tắc này sẽ giúp bạn giải quyết các bài toán liên quan đến đạo hàm một cách nhanh chóng và hiệu quả. Chúc bạn học tập tốt!