Bài 4.6 trang 94 SGK Toán 11 tập 1 thuộc chương trình học Toán 11, tập trung vào việc giải các phương trình lượng giác cơ bản. Bài tập này giúp học sinh rèn luyện kỹ năng biến đổi lượng giác và áp dụng các công thức để tìm nghiệm của phương trình.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu cho Bài 4.6 trang 94, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi G là trọng tâm của tam giác SCD.
Đề bài
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi G là trọng tâm của tam giác SCD.
a) Tim giao tuyến của hai mặt phẳng (SBG) và (SAC).
b) Tìm giao điểm của đường thằng BG và mặt phẳng (SAC).
Phương pháp giải - Xem chi tiết
a) Tìm giao tuyến của hai mặt phẳng (P) và (Q)
Tìm 2 điểm chung A, B của 2 mặt phẳng đó. AB chính là giao tuyến của (P) và (Q).
b) Tìm giao điểm của đường thẳng d và mặt phẳng (P)
Cách 1: Nếu (P) có chứa đường thẳng cắt d
Cách 2: Nếu (P) không chứa đường thẳng cắt d
+ Bước 1: Tìm \(\left( Q \right) \supset d\) và \(\left( P \right) \cap \left( Q \right) = a\)
+ Bước 2: Tìm \(I = a \cap d \Rightarrow I = d \cap \left( P \right)\)
Lời giải chi tiết
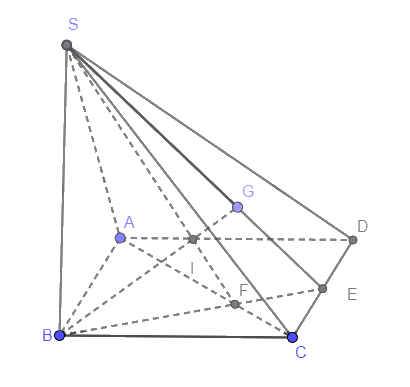
a) Gọi E là trung điểm của CD
Mà G là trọng tâm tam giác SCD nên G nằm trên SE.
Mở rộng (SBG) thành (SBE)
Trong (ABCD), gọi \(AC \cap BE = F\)
\(\begin{array}{l}\left\{ \begin{array}{l}AC \subset \left( {SAC} \right)\\BE \subset \left( {SBE} \right)\end{array} \right.\\ \Rightarrow F \in \left( {SAC} \right) \cap \left( {SBE} \right)\end{array}\)
\(\begin{array}{l} \Rightarrow SF = \left( {SAC} \right) \cap \left( {SBE} \right)\\ \Rightarrow SF = \left( {SAC} \right) \cap \left( {SBG} \right)\end{array}\)
b) Trong (SBE), gọi \(SF \cap AC = I\)
Mà: \(\left\{ \begin{array}{l}\left( {SAC} \right) \cap \left( {SBG} \right) = SF\\AC \subset \left( {SAC} \right)\end{array} \right. \Rightarrow I = BG \cap \left( {SAC} \right)\)
Bài 4.6 yêu cầu giải các phương trình lượng giác sau:
Phương trình tương đương với:
Vậy nghiệm của phương trình là x = -π/6 + k2π và x = 7π/6 + k2π (k ∈ Z).
Phương trình tương đương với:
Vậy nghiệm của phương trình là x = π/12 + kπ/2 và x = -5π/12 + kπ/2 (k ∈ Z).
Phương trình tương đương với:
Vậy nghiệm của phương trình là x = kπ (k ∈ Z).
Phương trình tương đương với:
Vậy nghiệm của phương trình là x = π/12 + kπ/3 (k ∈ Z).
Khi giải phương trình lượng giác, cần chú ý đến các điểm sau:
Việc giải phương trình lượng giác có nhiều ứng dụng trong thực tế, bao gồm:
Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh có thể tự tin giải Bài 4.6 trang 94 SGK Toán 11 tập 1 và các bài tập tương tự. Chúc các em học tốt!