Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 của giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 1 trang 81 và 82 sách giáo khoa Toán 11 tập 1.
Mục tiêu của chúng tôi là giúp các em hiểu rõ kiến thức, nắm vững phương pháp giải và tự tin làm bài tập về nhà. Hãy cùng bắt đầu nhé!
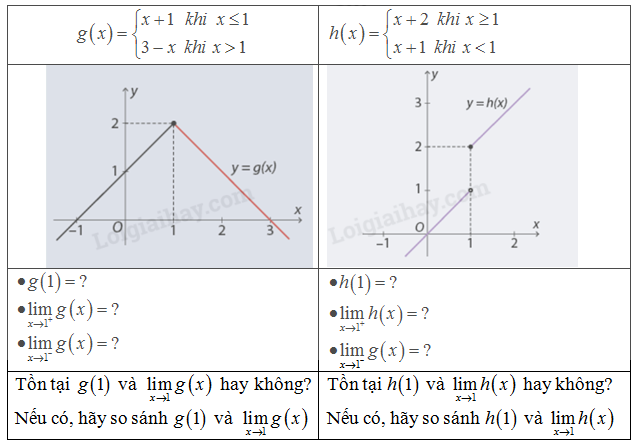
Dòng 1 của bảng dưới đây cho biết biểu thức của một hàm số. Dòng 2 cho biết đồ thị của hàm số đã cho. Trả lời các câu hỏi ở dòng 3 và 4
Dòng 1 của bảng dưới đây cho biết biểu thức của một hàm số. Dòng 2 cho biết đồ thị của hàm số đã cho. Trả lời các câu hỏi ở dòng 3 và 4
Phương pháp giải:
Với \(x = 1\) nên dựa vào điều kiện \(x \le 1\) để tính \(g\left( 1 \right)\) thì thay vào hàm số \(g\left( x \right) = x + 1\)
Với \(h\left( 1 \right)\) tính tương tự như \(g\left( 1 \right)\)
Khi \(x \to {1^ + }\) tức là \(x \ge 1\) nên phải tính\(\,\mathop {\lim }\limits_{x \to {1^ + }} g\left( x \right)\) ứng với hàm số \(g\left( x \right) = x + 1\)
Còn khi \(x \to {1^ - }\) tức là \(x < 1\) nên phải tính \(\,\mathop {\lim }\limits_{x \to {1^ - }} g\left( x \right)\) ứng với hàm số \(g\left( x \right) = 3 - x\)
Hàm \(h\left( x \right)\) thì làm tương tự như hàm \(g\left( x \right)\)
Lời giải chi tiết:

Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^2} - x - 6}}{{x + 2}}\,\,\,khi\,\,x \ne 2\\\,\,\,\,\,\,\,\,\,\,\,\,\,\, - 6\,\,\,khi\,\,x = - 2\end{array} \right.\). Xét tính liên tục của hàm số tại \({x_0} = - 2\)
Phương pháp giải:
Hàm số liên tục tại \({x_0} = - 2\) nếu \(\mathop {\lim }\limits_{x \to - 2} f\left( x \right) = f\left( { - 2} \right)\)
Đây là giới hạn tại điểm dạng vô định \(\frac{0}{0}\) nên phải thực hiện khử mẫu
Đây là hàm phân thức hữu tỉ nên ta thực hiện phân tích đa thức thành nhân tử để khử dạng vô định
Lời giải chi tiết:
Tập xác định của hàm số là \(\mathbb{R}\)
Khi \(x = - 2\), ta có \(f\left( { - 2} \right) = - 6\)
\(\mathop {\lim }\limits_{x \to - 2} f\left( x \right) = \mathop {\lim }\limits_{x \to - 2} \frac{{{x^2} - x - 6}}{{x + 2}} = \mathop {\lim }\limits_{x \to - 2} \frac{{\left( {x + 2} \right)\left( {x - 3} \right)}}{{x + 2}} = \mathop {\lim }\limits_{x \to - 2} \left( {x - 3} \right) = - 2 - 3 = - 5\)
Vì \( - 5 \ne - 6\) \( \Rightarrow \) \(\mathop {\lim }\limits_{x \to - 2} f\left( x \right) \ne f\left( { - 2} \right)\) do đó hàm số không liên tục tại \({x_0} = - 2\)
Xét tính liên tục của hàm số \(f\left( x \right) = {x^2} + 1\) tại điểm \({x_0}\) bất kì thuộc \(\mathbb{R}\)
Phương pháp giải:
Hàm số liên tục tại \(x = {x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
Lời giải chi tiết:
Tập xác định của hàm số là \(\mathbb{R}\)
Khi \(x = {x_0}\) thì \(f\left( {{x_0}} \right) = x_0^2 + 1\)
\(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \left( {{x^2} + 1} \right) = x_0^2 + 1 = f\left( {{x_0}} \right)\)
Vậy hàm số \(f\left( x \right)\) liên tục tại điểm \({x_0}\) bất kì thuộc \(\mathbb{R}\)
Xét tính liên tục của hàm số \(f\left( x \right) = \frac{{{x^2} - 1}}{{x - 1}}\) trên \(\left( {1; + \infty } \right)\)
Phương pháp giải:
Hàm số liên tục trên một khoảng nếu nó liên tục tại mọi điểm thuộc khoảng đó.
Lời giải chi tiết:
Hàm số có tập xác định là \(\left( { - \infty ;1} \right) \cup \left( {1; + \infty } \right)\)
Với mọi \({x_0} > 1\), ta có \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{{x^2} - 1}}{{x - 1}} = \frac{{x_0^2 - 1}}{{{x_0} - 1}} = f\left( {{x_0}} \right)\). Vậy hàm số liên tục tại mọi điểm \({x_0} > 1\) nên hàm số liên tục trên \(\left( {1; + \infty } \right)\)
Mục 1 của SGK Toán 11 tập 1 thường xoay quanh các khái niệm cơ bản về dãy số, cấp số cộng, cấp số nhân. Việc nắm vững kiến thức nền tảng này là vô cùng quan trọng để giải quyết các bài tập phức tạp hơn trong chương trình học. Bài viết này sẽ đi sâu vào từng bài tập trong mục 1, trang 81 và 82, cung cấp lời giải chi tiết và dễ hiểu.
Bài tập về dãy số thường yêu cầu học sinh xác định số hạng tổng quát của dãy, tính tổng các số hạng của dãy, hoặc chứng minh một tính chất nào đó của dãy. Để giải quyết những bài tập này, cần nắm vững các công thức và định lý liên quan đến dãy số.
Cấp số cộng là một dãy số đặc biệt trong đó hiệu của hai số hạng liên tiếp là một hằng số. Các bài tập về cấp số cộng thường yêu cầu học sinh tìm số hạng, công sai, hoặc tính tổng các số hạng của cấp số cộng.
Công thức quan trọng:
Cấp số nhân là một dãy số đặc biệt trong đó thương của hai số hạng liên tiếp là một hằng số. Các bài tập về cấp số nhân tương tự như cấp số cộng, nhưng sử dụng các công thức khác.
Công thức quan trọng:
Ví dụ 1: Cho cấp số cộng có số hạng đầu u1 = 2 và công sai d = 3. Tìm số hạng thứ 5 của cấp số cộng.
Lời giải: Sử dụng công thức un = u1 + (n-1)d, ta có u5 = 2 + (5-1) * 3 = 2 + 12 = 14.
Ví dụ 2: Cho cấp số nhân có số hạng đầu u1 = 1 và công bội q = 2. Tính tổng 4 số hạng đầu tiên của cấp số nhân.
Lời giải: Sử dụng công thức Sn = u1 * (1 - qn) / (1 - q), ta có S4 = 1 * (1 - 24) / (1 - 2) = (1 - 16) / (-1) = 15.
Hy vọng bài viết này đã giúp các em hiểu rõ hơn về cách giải các bài tập trong mục 1 trang 81, 82 SGK Toán 11 tập 1. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!