Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 tại giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 3 trang 60, 61, 62 của sách giáo khoa Toán 11 tập 2.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong các kỳ thi.
Cho hình hộp \(ABCD.A'B'C'D'\). Tìm hình chiều của các điểm \(A',C',D'\) lên mặt phẳng \(\left( {ABCD} \right)\) theo phương của đường thẳng \(BB'\)
Cho hình hộp \(ABCD.A'B'C'D'\). Tìm hình chiều của các điểm \(A',C',D'\) lên mặt phẳng \(\left( {ABCD} \right)\) theo phương của đường thẳng \(BB'\)
Phương pháp giải:
Tìm đường thẳng song song với đường thẳng \(BB'\) xuất phát từ các điểm \(A',C',D'\)
Lời giải chi tiết:
Hình chiếu lần lượt là \(A,C,D\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông. Biết rằng hình chiếu của \(S\) trên mặt phẳng \(\left( {ABCD} \right)\) là trung điểm \(H\) của cạnh \(AD\). Xác định hình chiếu của:
a) Tam giác \(SBC\) trên mặt phẳng \(\left( {ABCD} \right)\)
b) Các cạnh \(SB\) và \(SC\) trên mặt phẳng \(\left( {SAD} \right)\)
Phương pháp giải:
a) Tìm hình chiếu của \(S\) lên mặt phẳng \(\left( {ABCD} \right)\) là xong vì \(B,C \in \left( {ABCD} \right)\)
b) Chứng minh \(BA,CD \bot \left( {SAD} \right) \Rightarrow \)\(A,D\) là hình chiếu của \(B\) và \(C\) trên \(\left( {SAD} \right)\)
Lời giải chi tiết:

a) Ta có \(SH \bot \left( {ABCD} \right)\) nên \(H\) là hình chiếu vuông góc của \(S\) lên \(\left( {ABCD} \right)\)
Vì \(B,C \in \left( {ABCD} \right)\) nên hình chiếu của \(\Delta SBC\) lên \(\left( {ABCD} \right)\) là \(\Delta HBC\)
b) Vì \(SH \bot \left( {ABCD} \right) \Rightarrow SH \bot AB,SH \bot CD\)
Vì \(\left\{ \begin{array}{l}AB \bot SH\\AB \bot AD\end{array} \right. \Rightarrow AB \bot \left( {SAD} \right) \Rightarrow \) Hình chiếu vuông góc của \(B\) lên \(\left( {SAD} \right)\) là \(A\)
Vậy hình chiếu của \(SB\) lên \(\left( {SAD} \right)\) là \(SA\)
Vì \(\left\{ \begin{array}{l}CD \bot SH\\CD \bot AD\end{array} \right. \Rightarrow CD \bot \left( {SAD} \right) \Rightarrow \) Hình chiếu vuông góc của \(C\) lên \(\left( {SAD} \right)\) là \(D\)
Vậy hình chiếu của \(SC\) lên \(\left( {SAD} \right)\) là \(SD\)
Cho đường thẳng \(b\) không nằm trong mặt phẳng \(\left( \alpha \right)\) và không vuông góc với \(\left( \alpha \right)\). Gọi \(A,B\) là hai điểm phân biệt trên \(b\) và \(A',B'\) lần lượt là hình chiếu của \(A,B\) trên \(\left( \alpha \right)\). Gọi \(b'\) là đường thẳng đi qua \(A',B'\) thì \(b'\) là hình chiếu vuông góc của \(b\) trên mặt phẳng \(\left( \alpha \right)\). Xét \(a\) là một đường thẳng nằm tròn \(\left( \alpha \right)\).
a) Nếu \(a \bot b'\) thì \(a\) có vuông góc với \(b\) không? Vì sao?
b) Nếu \(a \bot b\) thì \(a\) có vuông góc với \(b'\) không? Vì sao?

Phương pháp giải:
Chứng minh \(a \bot AA'\)
Chứng minh \(a \bot \left( {AA'B'B} \right)\) từ đó suy ra \(a \bot b'\) và \(a \bot b\)
Lời giải chi tiết:
a) Vì \(\left\{ \begin{array}{l}AA' \bot \left( \alpha \right)\\a \subset \left( \alpha \right)\end{array} \right. \Rightarrow AA' \bot a\)
Vì \(\left\{ \begin{array}{l}a \bot b'\\a \bot AA'\end{array} \right. \Rightarrow a \bot \left( {AA'B'B} \right)\). Mà \(b \subset \left( {AA'B'B} \right) \Rightarrow a \bot b\)
b) Vì \(\left\{ \begin{array}{l}AA' \bot \left( \alpha \right)\\a \subset \left( \alpha \right)\end{array} \right. \Rightarrow AA' \bot a\)
Vì \(\left\{ \begin{array}{l}a \bot b\\a \bot AA'\end{array} \right. \Rightarrow a \bot \left( {AA'B'B} \right)\). Mà \(b' \subset \left( {AA'B'B} \right) \Rightarrow a \bot b'\)
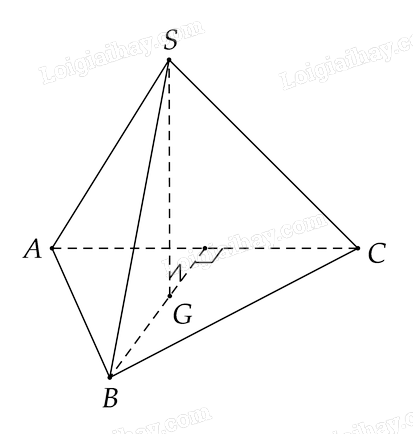
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác cân đỉnh \(B\) và hình chiếu của \(S\) trên mặt phẳng \(\left( {ABC} \right)\) là trọng tâm của tam giác \(ABC\). Chứng minh rằng các đường thẳng \(AC\) và \(SB\) vuông góc với nhau.
Phương pháp giải:
Lấy \(G\) là trọng tâm của \(\Delta ABC\). Chứng minh \(BG\) là hình chiếu vuông góc của \(SB\) xuống \(\left( {ABC} \right)\) kết hợp với \(AC \bot BG\) từ đó suy ra \(AC \bot SB\)
Lời giải chi tiết:

Gọi \(G\) là trọng tâm của \(\Delta ABC\). Ta có \(SG \bot \left( {ABC} \right)\) (gt), suy ra \(BG\) là hình chiếu vuông góc của \(SG\) xuống \(\left( {ABC} \right)\) \(\left( 1 \right)\)
Vì \(\Delta \)\(ABC\) cân tại \(B\) suy ra \(BG \bot AC\) \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), suy ra \(AC \bot SB\) (định lý ba đường vuông góc)
Mục 3 trong SGK Toán 11 tập 2 thường tập trung vào một chủ đề cụ thể, ví dụ như phép biến hình, hàm số lượng giác, hoặc các ứng dụng của đạo hàm. Việc nắm vững kiến thức lý thuyết và kỹ năng giải bài tập trong mục này là rất quan trọng để hiểu sâu hơn về chương trình học và chuẩn bị tốt cho các bài kiểm tra.
Để giúp các em học sinh hiểu rõ hơn về nội dung bài học, chúng tôi sẽ giải chi tiết từng bài tập trong mục 3 trang 60, 61, 62. Mỗi bài giải sẽ bao gồm:
Lời giải:
Hàm số y = √(2 - cos x) xác định khi và chỉ khi 2 - cos x ≥ 0. Vì -1 ≤ cos x ≤ 1 nên 2 - cos x ≥ 2 - 1 = 1 > 0 với mọi x. Vậy tập xác định của hàm số là R.
Lời giải:
Ta có sin 2x = 2sin x cos x. Vậy phương trình trở thành 2sin x cos x = cos x. Chuyển vế, ta được 2sin x cos x - cos x = 0. Phân tích thành nhân tử, ta có cos x (2sin x - 1) = 0. Suy ra cos x = 0 hoặc 2sin x - 1 = 0.
Vậy nghiệm của phương trình là x = π/2 + kπ, x = π/6 + k2π, x = 5π/6 + k2π, k ∈ Z.
Để học tập và giải bài tập Toán 11 tập 2 hiệu quả, các em nên:
Kiến thức trong mục 3 có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, như vật lý, kỹ thuật, kinh tế và khoa học máy tính. Ví dụ, hàm số lượng giác được sử dụng để mô tả các hiện tượng dao động, sóng và ánh sáng. Đạo hàm được sử dụng để tính tốc độ thay đổi của các đại lượng và tối ưu hóa các quá trình.
Hy vọng rằng với lời giải chi tiết và các hướng dẫn hữu ích trên đây, các em học sinh sẽ tự tin hơn trong việc học tập và giải bài tập Toán 11 tập 2. Chúc các em học tốt!