Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 của giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 1 trang 64 và 65 của sách giáo khoa Toán 11 tập 2.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài toán, nắm vững phương pháp giải và tự tin làm bài tập. Hãy cùng bắt đầu nhé!
Quan sát Hình 8.28, trả lời các câu hỏi:
Quan sát Hình 8.28, trả lời các câu hỏi:
a) Bốn cánh cửa kính 1, 2, 3, 4 (Hình 8.28) chia không gian thành bao nhiêu phần?
b) Bạn An (nữ, áo vàng) và bạn Bình (nam, áo xanh) ở phần không gian nào?
Phương pháp giải:
Quan sát hình ảnh.
Lời giải chi tiết:
a) Bốn cánh cửa kính chia không gian thành 4 phần.
b) Bạn An ở phần không gian chứa cánh cửa số 1 và 4, Bình ở phần không gian chứa cánh cửa số 1 và 2.
Cho nhị diện \(\left[ {\alpha ,a,\beta } \right]\) và điểm O thuộc a. Vẽ mặt phẳng (P) qua O và vuông góc a. Gọi giao tuyển của (P) với các nửa mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) lần lượt là các tia Ox, Oy. Hỏi số đo góc xOy thay đổi như thế nào khi điểm O thay đổi trên a?

Phương pháp giải:
Quan sát hình vẽ.
Lời giải chi tiết:
Số đo góc xOy không thay đổi khi điểm O thay đổi trên A.
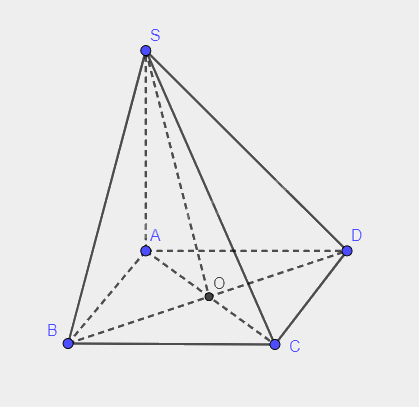
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD), \(SA = \frac{{\sqrt 2 }}{2}a\). Tính số đo của các góc nhị diện \(\left[ {S,BD,A} \right]\), \(\left[ {S,BD,C} \right]\).
Phương pháp giải:
Cách tìm số đo của góc nhị diện \(\left[ {S,CD,A} \right]\):
+ Tìm giao tuyến d của (SCD) và (ACD).
+ Tìm \(a \subset \left( {SCD} \right)\) vuông góc với d. Tìm \(b \subset \left( {ACD} \right)\) vuông góc với d.
+ Tính \(\left( {a,b} \right)\).
Lời giải chi tiết:

SA vuông góc với BD (Vì SA vuông góc với (ABCD))
AC vuông với BD (Vì ABCD là hình vuông)
Nên (SAC) vuông với BD
Trong (ABCD), gọi O là giao điểm của AC và BD
Suy ra SO vuông góc với BD
Mà: AO vuông góc với BD
Suy ra góc phẳng nhị diện \(\left[ {S,BD,A} \right]\) là góc SOA
ABCD là hình vuông cạnh a nên AC bằng \(\sqrt 2 a\). Suy ra AO = \(\frac{{\sqrt 2 }}{2}a\)
\(\tan \widehat {SOA} = \,\frac{{SA}}{{AO}} = \frac{{\frac{{\sqrt 2 }}{2}a}}{{\frac{{\sqrt 2 }}{2}a}} = 1 \Rightarrow \widehat {SOA} = {45^0}\)
Ta có: SO vuông góc với BD, CO vuông góc với BD nên góc phẳng nhị diện \(\left[ {S,BD,C} \right]\) là góc SOC
\(\widehat {SOC} = {180^0} - {45^0} = {135^0}\)
Mục 1 của SGK Toán 11 tập 2 thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này một cách hiệu quả, học sinh cần nắm vững kiến thức lý thuyết liên quan, hiểu rõ các định nghĩa, định lý và công thức quan trọng. Đồng thời, việc luyện tập thường xuyên với các bài tập khác nhau cũng rất cần thiết để củng cố kiến thức và rèn luyện kỹ năng giải toán.
Chúng ta sẽ đi vào giải chi tiết từng bài tập trong mục 1 trang 64 và 65. Lưu ý rằng, mỗi bài tập có thể yêu cầu vận dụng các kiến thức và kỹ năng khác nhau. Do đó, học sinh cần đọc kỹ đề bài, xác định đúng yêu cầu và lựa chọn phương pháp giải phù hợp.
Đề bài: (Nêu rõ đề bài)
Lời giải:
Giải thích: (Giải thích chi tiết từng bước giải, làm rõ lý do tại sao lại thực hiện như vậy)
Đề bài: (Nêu rõ đề bài)
Lời giải:
Giải thích: (Giải thích chi tiết từng bước giải, làm rõ lý do tại sao lại thực hiện như vậy)
Đề bài: (Nêu rõ đề bài)
Lời giải:
(Giải chi tiết bài toán)
Giải thích: (Giải thích chi tiết từng bước giải, làm rõ lý do tại sao lại thực hiện như vậy)
Sau khi giải xong các bài tập trong SGK, các em có thể tự tìm thêm các bài tập tương tự để luyện tập. Ngoài ra, các em cũng có thể tham khảo các tài liệu tham khảo khác để mở rộng kiến thức và nâng cao kỹ năng giải toán. Việc tự học và khám phá là rất quan trọng để các em có thể đạt được kết quả tốt nhất trong môn Toán.
Để hỗ trợ quá trình học tập và giải bài tập, các em có thể tham khảo các tài liệu sau:
Hy vọng rằng, với những hướng dẫn chi tiết và lời giải cụ thể trong bài viết này, các em học sinh đã có thể tự tin giải các bài tập trong mục 1 trang 64, 65 SGK Toán 11 tập 2. Chúc các em học tập tốt và đạt được kết quả cao trong môn Toán!