Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11 tập 2. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Với mục tiêu giúp các em học sinh nắm vững kiến thức và đạt kết quả tốt trong môn Toán, chúng tôi đã biên soạn bộ giải bài tập SGK Toán 11 tập 2 trang 48, 49 một cách cẩn thận và đầy đủ.
Dân số của thành phố A tăng theo từng năm kể từ năm 2000 đến nay.
Dân số của thành phố A tăng theo từng năm kể từ năm 2000 đến nay. Giả sử số dân của thành phố trên được ước tính bởi công thức \(f\left( t \right) = \frac{{30t + 18}}{{t + 6}}\) (nghìn người), trong đó \(t\) là số năm kể từ năm \(2000\). Chẳng hạn, ở thời điểm năm 2020 thì \(t = 2020 - 2000 = 20\).
a) Nếu xem \(y = f\left( t \right)\) là hàm số xác định trên nửa khoảng \(\left[ {0; + \infty } \right)\) thì đạo hàm của nó biểu thị cho đại lượng nào?
b) Tính tốc độ tăng dân số của thành phố A vào năm 2005 và 2010 (làm tròn kết quả đến hàng phần trăm). Vào năm nào trong hai năm nêu trên, dân số của thành phố A tăng nhanh hơn?
c) Vào năm nào thì tốc độ tăng dân số đạt mức 0,5 nghìn người/năm?
Phương pháp giải:
a) Áp dụng \(s'\left( t \right) = v\left( t \right)\) nên \(f'\left( t \right)\) sẽ biểu thị cho tốc độ tăng dân số.
b) Áp dụng công thức tính \(\left( {\frac{u}{v}} \right)' = \frac{{u'.v - v'.u}}{{{v^2}}}\)
Thay \(t\) tìm được vào \(f'\left( t \right)\) là ta tìm được tốc độ tăng dân số của thành phố A vào năm đó
c) Giải phương trình \(f'\left( t \right) = 0,5\)
Lời giải chi tiết:
a) \(f'\left( t \right)\) biểu thị cho tốc độ tăng dân số của thành phố A
b) Ta có \(f'\left( t \right) = \frac{{\left( {30t + 18} \right)'.\left( {t + 6} \right) - \left( {t + 6} \right)'.\left( {30t + 18} \right)}}{{{{\left( {t + 6} \right)}^2}}} = \frac{{30\left( {t + 6} \right) - \left( {30t + 18} \right)}}{{{{\left( {t + 6} \right)}^2}}} = \frac{{162}}{{{{\left( {t + 6} \right)}^2}}}\)
+) Với năm \(2005\) thì \(t = 2005 - 2000 = 5\).
Suy ra tốc độ tăng dân số là \(f'\left( 5 \right) = \frac{{162}}{{{{\left( {5 + 6} \right)}^2}}} = \frac{{162}}{{121}} \approx 1,34\)nghìn người/năm
+) Với năm 2010 thì \(t = 2010 - 2000 = 10\)
Suy ra tốc độ tăng dân số là \(f'\left( {10} \right) = \frac{{162}}{{{{\left( {10 + 6} \right)}^2}}} \approx 0,63\)nghìn người/năm
c) Để tốc độ tăng dân số đạt mức \(0,5\) nghìn người/năm là
\(f'\left( t \right) = 0,5 \Leftrightarrow \frac{{162}}{{{{\left( {t + 6} \right)}^2}}} = 0,5 \Leftrightarrow {\left( {t + 6} \right)^2} = 324 \Leftrightarrow t + 6 = 18 \Leftrightarrow t = 12\)
Vậy năm \(2012\) thì tốc độ tăng dân số đạt mức \(0,5\) nghìn người/năm
Một bể chứa nước đang chứa \(20{m^3}\) nước. Một người cần lấy nước để sử dụng nên đã mở van ở đáy bể để nước chảy vào thùng chứa. Giả sử thể tích nước trong thùng chứa tăng dần theo thời gian và được ước tính bởi hàm số \(V\left( t \right) = t - \frac{1}{{80}}{t^2}\,\,\,\left( {0 \le t \le 40} \right)\).
a) Có thể xem tốc độ nước chảy vào thùng bằng với tốc độ tăng của thể tích nước trong thùng. Tính tốc độ nước chảy vào thùng chứa tại thời điểm \(t = 5\) phút và \(t = 15\) phút.
b) Nước chảy vào thùng chứa nhanh nhất tại thời điểm nào?
Phương pháp giải:
a) Vì tốc độ nước chảy vào thùng bằng với tốc độ tăng của thể tích nước trong thùng nên tốc độ nước chảy vào thùng là \(V\left( t \right) = t - \frac{1}{{80}}{t^2}\)
b) Biến đổi \(V\left( t \right)\) về dạng bình phương
Lời giải chi tiết:
a) Vì tốc độ nước chảy vào thùng bằng với tốc độ tăng của thể tích nước trong thùng nên tốc độ nước chảy vào thùng là \(V\left( t \right) = t - \frac{1}{{80}}{t^2}\)
\(V\left( 5 \right) = 5 - \frac{1}{{80}}{.5^2} = 4,6875\) \({m^3}\)/phút
\(V\left( {15} \right) = 15 - \frac{1}{{80}}{.15^2} = 12,1875\)\({m^3}\)/phút
b) Ta có \(V\left( t \right) = - \frac{1}{{80}}\left( {{t^2} - 80t} \right) = - \frac{1}{{80}}{\left( {t - 40} \right)^2} + 20 \le 20\)
Dấu “=” xảy ra khi và chỉ khi \(t - 40 = 0 \Leftrightarrow t = 40\)
Vậy tại thời điểm \(t = 40\) thì nước chảy vào thùng nhanh nhất
Để đo lường khả năng nắm vững kiến thức của sinh viên sau khi kết thức khóa học, một nhà nghiên cứu tiến hành cho sinh viên làm bài kiểm tra mỗi tháng trong vòng 12 tháng kể từ ngày kết thức khóa học. Giả sử điểm số trung bình \(s\left( t \right)\) của các sinh viên đạt được trong bài kiểm tra ở tháng thứ \(t\) được tính bởi \(s\left( t \right) = 7.{e^{ - 0,2t}} + 1\) với \(s\left( t \right)\) tính bằng điểm, \(0 \le t \le 12\). Nếu xem \(y = s\left( t \right)\) là hàm số xác định trên \(\left[ {0;12} \right]\) thì \(\left| {s'\left( t \right)} \right|\) biểu thị tốc độ giẩm điểm số tại tháng thứ \(t\) trong đợt khảo sát.
Tính tốc độ giảm điểm số tại \(t = 2\) và \(t = 6\). Tại thời điểm nào trong hai thời điểm trên, điểm số của các sinh viên được khảo sát giảm nhanh hơn?
Phương pháp giải:
Tính đạo hàm của hàm số \(s\left( t \right)\).
Áp dụng công thức \(\left( {{e^u}} \right)' = u'.{e^u}\)
Thay \(t = 2;t = 6\) vào \(\left| {s'\left( t \right)} \right|\) ta tìm được tốc độ giảm điểm số
Lời giải chi tiết:
Ta có \(s'\left( t \right) = \left( {7{e^{ - 0,2t}} + 1} \right)' = 7.{e^{ - 0,2t}}.\left( { - 0,2t} \right)' = - 1,4.{e^{ - 0,2t}}\)
\( \Rightarrow \left| {s'\left( t \right)} \right| = 1,4.{e^{ - 0,2t}}\) là tốc độ giảm điểm số tại tháng thứ \(t\)
+) Với \(t = 2\) thì tốc độ giảm điểm số là \(1,4.{e^{ - 0,2.2}} \approx 0,9384\)
+) Với \(t = 6\) thì tốc độ giảm điểm số là \(1,4.{e^{ - 0,2.6}} \approx 0,4217\)
Vậy tại thời điểm \(t = 2\) thì điểm số của sinh viên được khảo sát giảm nhanh hơn
Cân nặng của một bé gái trong độ tuổi từ 0 đến 36 tháng được ước tính bởi hàm số \(y = f\left( t \right) = 0,00031{t^3} - 0,02396{t^2} + 0,76806t + 3,3\) và có đồ thị như sau (nguồn: https://www.vinmec.com):
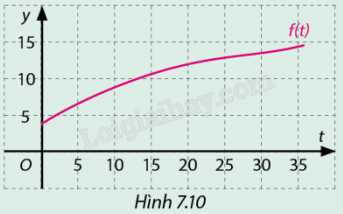
a) Tính tốc độ tăng cân nặng của bé gái tại thời điểm 5 tháng tuổi.
b) Trong ba thời điểm \(t = 5;t = 10;t = 15\), thời điểm nào cân nặng bé gái tăng nhanh nhất?
Phương pháp giải:
a) Tốc độ tăng cân nặng chính là đạo hàm của hàm \(f\left( t \right)\)
b) Thay \(t = 5;t = 10;t = 15\) vào đạo hàm của hàm \(f\left( t \right)\)
Lời giải chi tiết:
a) Tốc độ tăng cân nặng là \(f'\left( t \right) = 0,00093{t^2} - 0,04792t + 0,76806\)
Vậy tốc tăng cân nặng của bé gái tại thời điểm \(5\) tháng tuổi là
\(f'\left( 5 \right) = 0,55171\)
b) Tại thời điểm \(t = 5\) là \(f'\left( 5 \right) = 0,55171\)
Tại thời điểm \(t = 10\) là \(f'\left( {10} \right) = 0,38186\)
Tại thời điểm \(t = 15\) là \(f'\left( {15} \right) = 0,25851\)
Vậy tại thời điểm \(t = 5\) tháng là cân nặng của bé gái tăng nhanh nhất.
Trang 48 và 49 của SGK Toán 11 tập 2 thường tập trung vào các chủ đề quan trọng như phép biến hình, vector, và các ứng dụng của chúng trong hình học. Các bài tập trong phần này thường yêu cầu học sinh vận dụng kiến thức về các phép biến hình (tịnh tiến, quay, đối xứng) để chứng minh tính chất của các hình, hoặc giải các bài toán liên quan đến vector.
Các bài tập trang 48 thường xoay quanh việc xác định ảnh của một điểm, một đường thẳng, một hình qua phép biến hình. Để giải quyết các bài tập này, học sinh cần nắm vững định nghĩa và tính chất của từng phép biến hình. Ví dụ:
Trang 49 thường tập trung vào các bài tập ứng dụng của phép biến hình để chứng minh tính chất của các hình. Các bài tập này đòi hỏi học sinh phải có khả năng phân tích hình học và vận dụng linh hoạt các kiến thức đã học. Ví dụ:
Để giải các bài tập trang 48, 49 SGK Toán 11 tập 2 một cách hiệu quả, học sinh cần:
Bài tập: Cho điểm A(1, 2) và vector v = (3, -1). Tìm tọa độ điểm A' là ảnh của A qua phép tịnh tiến theo vector v.
Giải:
Áp dụng công thức phép tịnh tiến, ta có:
x' = x + a = 1 + 3 = 4
y' = y + b = 2 + (-1) = 1
Vậy, tọa độ điểm A' là (4, 1).
Khi giải các bài tập về phép biến hình, học sinh cần chú ý đến các yếu tố sau:
Giaitoan.edu.vn cam kết cung cấp cho bạn những lời giải chi tiết, dễ hiểu và chính xác nhất cho các bài tập SGK Toán 11 tập 2. Chúng tôi hy vọng rằng với sự hỗ trợ của chúng tôi, bạn sẽ học tập môn Toán một cách hiệu quả và đạt được kết quả tốt nhất.