Bài 4.36 trang 125 SGK Toán 11 tập 1

Bài 4.36 trang 125 SGK Toán 11 tập 1 - Cùng khám phá

Bài 4.36 thuộc chương trình Toán 11 tập 1, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh hiểu rõ các quy tắc tính đạo hàm và cách áp dụng chúng vào việc tìm cực trị của hàm số.

Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 4.36 trang 125 SGK Toán 11 tập 1, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.

Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi I , J lần lượt là trung điểm của AB và CB.

Đề bài

Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi I , J lần lượt là trung điểm của AB và CB. Giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng song song với

A. Đường thẳng AD.

B. Đường thẳng BJ.

C. Đường thẳng BI.

D. Đường thẳng IJ.

Phương pháp giải - Xem chi tiết Bài 4.36 trang 125 SGK Toán 11 tập 1 - Cùng khám phá 1

(P) và (Q) có điểm chung A, chứa lần lượt 2 đường thẳng a, b song song với nhau thì giao tuyến của (P) và (Q) là đường thẳng đi qua A, song song với a, b.

Lời giải chi tiết

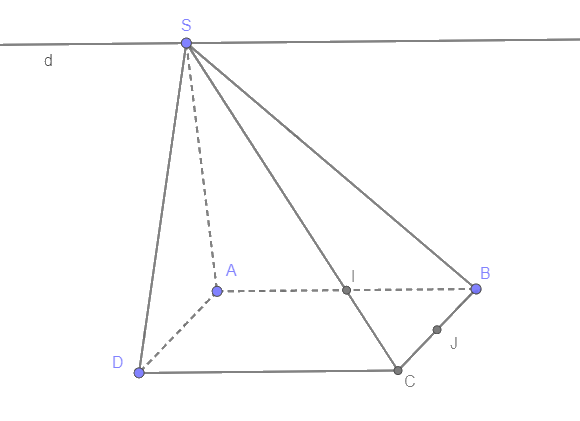
Bài 4.36 trang 125 SGK Toán 11 tập 1 - Cùng khám phá 2

(SAB) và (SCD) có chung điểm S, lần lượt chứa 2 đường thẳng AB và CD song sogn với nhau nên giao tuyến của 2 mặt phẳng là đường thẳng đi qua S và song song với AB hay BI.

Chọn đáp án C.

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Bài 4.36 trang 125 SGK Toán 11 tập 1 - Cùng khám phá – hành trang không thể thiếu trong chuyên mục Học tốt Toán lớp 11 trên nền tảng soạn toán. Bộ bài tập lý thuyết toán thpt được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Bài 4.36 trang 125 SGK Toán 11 tập 1 - Giải chi tiết và hướng dẫn

Bài 4.36 trang 125 SGK Toán 11 tập 1 là một bài tập quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững kiến thức về đạo hàm và ứng dụng của nó trong việc tìm cực trị hàm số. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:

Nội dung bài toán

Bài 4.36 thường yêu cầu học sinh tìm cực trị của một hàm số cho trước. Để giải bài toán này, chúng ta cần thực hiện các bước sau:

Tính đạo hàm cấp một (f'(x)) của hàm số.
Tìm các điểm dừng bằng cách giải phương trình f'(x) = 0.
Lập bảng biến thiên để xác định khoảng đồng biến, nghịch biến của hàm số.
Xác định cực đại, cực tiểu dựa vào dấu của đạo hàm cấp hai (f''(x)) hoặc dựa vào bảng biến thiên.

Lời giải chi tiết

Ví dụ: Giả sử hàm số cần tìm cực trị là f(x) = x³ - 3x² + 2.

Tính đạo hàm cấp một: f'(x) = 3x² - 6x.
Tìm điểm dừng: Giải phương trình 3x² - 6x = 0, ta được x = 0 và x = 2.
Tính đạo hàm cấp hai: f''(x) = 6x - 6.
Xác định cực trị:

Tại x = 0: f''(0) = -6 < 0, hàm số đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2.
Tại x = 2: f''(2) = 6 > 0, hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2.

Lưu ý quan trọng

Khi giải bài tập về cực trị hàm số, cần lưu ý các điểm sau:

Kiểm tra điều kiện xác định của hàm số.
Đảm bảo đạo hàm cấp một tồn tại tại các điểm dừng.
Sử dụng đúng các quy tắc tính đạo hàm.
Phân tích kỹ bảng biến thiên để xác định chính xác cực đại, cực tiểu.

Các bài tập tương tự

Để củng cố kiến thức về cực trị hàm số, bạn có thể luyện tập thêm các bài tập tương tự sau:

Bài 4.37 trang 125 SGK Toán 11 tập 1
Bài 4.38 trang 126 SGK Toán 11 tập 1
Các bài tập trong sách bài tập Toán 11 tập 1

Ứng dụng của việc tìm cực trị hàm số

Việc tìm cực trị hàm số có nhiều ứng dụng trong thực tế, chẳng hạn như:

Trong kinh tế: Tìm điểm tối ưu để đạt lợi nhuận cao nhất hoặc chi phí thấp nhất.
Trong kỹ thuật: Tìm kích thước tối ưu của một vật thể để đảm bảo độ bền hoặc hiệu quả cao nhất.
Trong khoa học: Tìm điểm cực trị của một hiện tượng vật lý để hiểu rõ hơn về bản chất của nó.

Kết luận

Bài 4.36 trang 125 SGK Toán 11 tập 1 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về đạo hàm và ứng dụng của nó trong việc tìm cực trị hàm số. Hy vọng với lời giải chi tiết và hướng dẫn trên, bạn sẽ tự tin giải bài tập này và các bài tập tương tự.

Hãy truy cập giaitoan.edu.vn để xem thêm nhiều bài giải Toán 11 tập 1 và các môn học khác.