Bài 4.33 trang 124 SGK Toán 11 tập 1 là một bài toán quan trọng trong chương trình học, yêu cầu học sinh vận dụng kiến thức về vectơ, phương trình đường thẳng và mặt phẳng để giải quyết. Bài toán này thường xuất hiện trong các đề thi và kiểm tra, do đó việc nắm vững phương pháp giải là rất cần thiết.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu cho Bài 4.33 trang 124 SGK Toán 11 tập 1, giúp các em học sinh hiểu rõ bản chất của bài toán và rèn luyện kỹ năng giải toán.
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi M là trung điểm của SC. Gọi I là giao điểm của dường thẳng AM và mặt phẳng (SBD). Mệnh đề nào sau đây đúng?
Đề bài
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi M là trung điểm của SC. Gọi I là giao điểm của dường thẳng AM và mặt phẳng (SBD). Mệnh đề nào sau đây đúng?
A. IA = 3IM.
B. IM = 3IA.
C. IM = 2IA.
D. IA = 2IM.
Phương pháp giải - Xem chi tiết
Cách tìm giao điểm của đường thẳng a và mặt phẳng (P):
+ Bước 1: Chọn mặt phẳng (Q) chứa a. Tìm giao tuyến d của (P) và (Q)
+ Bước 2: Tìm giao điểm I của a và d. I chính là giao điểm của d và (P).
Lời giải chi tiết
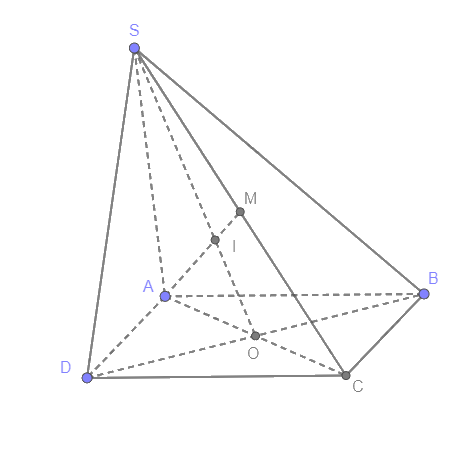
Trong (ABCD), gọi O là giao điểm của AC và BD
Trong (SAC), gọi I là giao điểm của AM và SO
Mà SO nằm trong (SBD) nên I là giao điểm của AM và (SBD)
Hình bình hành ABCD có O là giao điểm của AC và BD nên O là trung điểm AC, BD
Xét tam giác SAC có AM, SO là trung tuyến nên I là trọng tâm
Vậy IA = 2IM
Chọn đáp án D.
Bài 4.33 trang 124 SGK Toán 11 tập 1 thuộc chương trình Hình học không gian, cụ thể là phần đường thẳng và mặt phẳng trong không gian. Bài toán này thường yêu cầu học sinh xác định mối quan hệ giữa đường thẳng và mặt phẳng, hoặc tìm giao điểm của chúng. Để giải quyết bài toán này một cách hiệu quả, cần nắm vững các kiến thức cơ bản sau:
Để giải bài 4.33 trang 124 SGK Toán 11 tập 1, chúng ta cần phân tích kỹ đề bài để xác định các yếu tố quan trọng như:
Sau khi phân tích đề bài, chúng ta sẽ áp dụng các kiến thức và công thức đã học để giải quyết bài toán.
(Nội dung lời giải chi tiết sẽ được trình bày tại đây, bao gồm các bước giải cụ thể, giải thích rõ ràng và sử dụng các ký hiệu toán học chính xác. Ví dụ:)
Ví dụ: Giả sử bài toán yêu cầu tìm giao điểm của đường thẳng d: x = 1 + t, y = 2 - t, z = 3 + 2t và mặt phẳng (P): 2x - y + z = 5.
Ngoài bài 4.33 trang 124 SGK Toán 11 tập 1, còn rất nhiều bài tập tương tự về đường thẳng và mặt phẳng. Để giải quyết các bài tập này, chúng ta có thể áp dụng các phương pháp sau:
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, các em học sinh nên luyện tập thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Giaitoan.edu.vn cung cấp một kho bài tập phong phú và đa dạng, giúp các em học sinh tự tin hơn trong quá trình học tập.
Bài 4.33 trang 124 SGK Toán 11 tập 1 là một bài toán quan trọng, giúp học sinh hiểu rõ hơn về mối quan hệ giữa đường thẳng và mặt phẳng trong không gian. Việc nắm vững kiến thức và phương pháp giải bài toán này sẽ là nền tảng vững chắc cho các em học sinh trong quá trình học tập môn Toán.