Bài 8.13 trang 72 SGK Toán 11 tập 2 là một bài tập quan trọng trong chương trình học Toán 11, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, cùng với các phương pháp giải nhanh chóng và hiệu quả, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, \(SA = \sqrt 3 a\), \(SA \bot \left( {ABCD} \right)\). Tính số đo của góc nhị diện \(\left[ {S,CD,A} \right]\).
Đề bài
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, \(SA = \sqrt 3 a\), \(SA \bot \left( {ABCD} \right)\). Tính số đo của góc nhị diện \(\left[ {S,CD,A} \right]\).
Phương pháp giải - Xem chi tiết
Cách tìm số đo của góc nhị diện \(\left[ {S,CD,A} \right]\):
+ Tìm giao tuyến d của (SCD) và (ACD).
+ Tìm \(a \subset \left( {SCD} \right)\) vuông góc với CD. Tìm \(b \subset \left( {ACD} \right)\) vuông góc với CD.
+ Tính \(\left( {a,b} \right)\).
Lời giải chi tiết
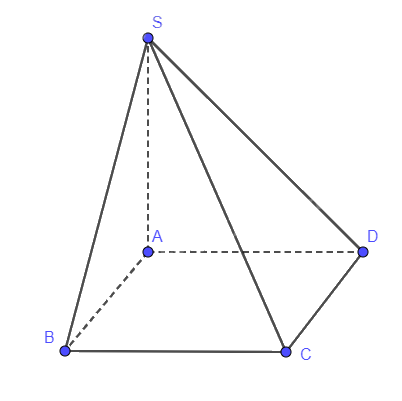
SA vuông góc với CD (Vì \(SA \bot \left( {ABCD} \right)\))
AD vuông góc với CD
Nên (SAD) vuông góc với CD
Suy ra SD vuông góc với CD
Vậy góc phẳng nhị diện \(\left[ {S,CD,A} \right]\) là góc SDA
\(\tan \widehat {SDA} = \frac{{SA}}{{AD}} = \frac{{\sqrt 3 a}}{a} = \sqrt 3 \Rightarrow \widehat {SDA} = {60^0}\)
Bài 8.13 trang 72 SGK Toán 11 tập 2 yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết một bài toán cụ thể. Bài toán thường liên quan đến việc tìm đạo hàm, xét dấu đạo hàm để xác định khoảng đồng biến, nghịch biến của hàm số, hoặc tìm cực trị của hàm số.
Trước khi bắt đầu giải bài toán, điều quan trọng nhất là phải đọc kỹ đề bài, hiểu rõ yêu cầu của bài toán và xác định các thông tin đã cho. Trong bài 8.13, cần xác định hàm số cần xét, khoảng xác định của hàm số và yêu cầu cụ thể của bài toán (ví dụ: tìm đạo hàm, tìm cực trị, xét tính đơn điệu).
Để giải bài toán đạo hàm, cần nắm vững các công thức đạo hàm cơ bản và các quy tắc tính đạo hàm (quy tắc cộng, trừ, nhân, chia, đạo hàm hợp). Ngoài ra, cần biết cách sử dụng đạo hàm để xét tính đơn điệu của hàm số và tìm cực trị.
(Giả sử đề bài là: Cho hàm số y = x3 - 3x2 + 2. Tìm khoảng đồng biến, nghịch biến và cực trị của hàm số.)
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + |
Từ bảng xét dấu, ta thấy:
Khi giải bài toán đạo hàm, cần chú ý các điểm sau:
Đạo hàm có rất nhiều ứng dụng trong thực tế, chẳng hạn như:
Việc nắm vững kiến thức về đạo hàm không chỉ giúp học sinh giải quyết các bài toán trong sách giáo khoa mà còn mở ra nhiều cơ hội ứng dụng trong các lĩnh vực khác nhau.
Hy vọng với lời giải chi tiết và phương pháp giải bài tập Bài 8.13 trang 72 SGK Toán 11 tập 2 này, các bạn học sinh sẽ hiểu rõ hơn về kiến thức đạo hàm và tự tin hơn trong quá trình học tập.