Bài 3.13 trang 79 SGK Toán 11 tập 1 là một bài tập quan trọng trong chương trình học Toán 11. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu và phương pháp giải bài tập Bài 3.13 trang 79 SGK Toán 11 tập 1, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Trong Vật lí, tỉ số giữa tốc độ c của ánh sáng trong chân không và của tốc độ v của ánh sáng trong một môi trường được gọi là chiết suất của môi trường đó. Chiết suất của một môi trường đồng nhất là không đổi.
Đề bài
Trong Vật lí, tỉ số giữa tốc độ c của ánh sáng trong chân không và của tốc độ v của ánh sáng trong một môi trường được gọi là chiết suất của môi trường đó. Chiết suất của một môi trường đồng nhất là không đổi. Ngày nay, với công nghệ nano, người ta tạo ra được các bản thủy tinh mà chiết suất của nó thay đổi theo một phương nào đó. Xét sự truyền của ánh sáng vào bản thủy tinh dọc theo trục Ox như Hình 3.9. Biết chiết suất của bản thủy tinh này thay đổi theo hoành độ x cho bởi: \(n\left( x \right) = \frac{a}{{a - x}}\) với \(0 \le x \le d\), trong đó \(a\) là một hằng số có giá trị lớn hơn bề dày \(d\) của bản thủy tinh.
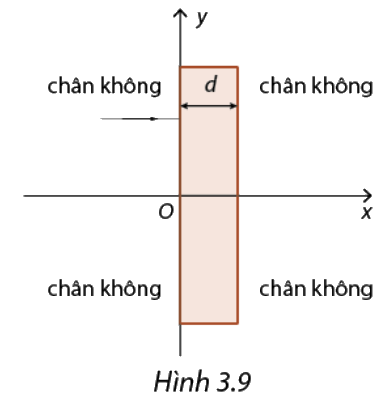
a) Chứng minh rằng tốc độ của ánh sáng cho bởi: \(v\left( x \right) = \left\{ \begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,c\,\,\,\,\,\,khi\,\,x < 0\\c\left( {1 - \frac{x}{a}} \right)\,\,\,\,\,\,khi\,\,\,0 \le x \le d\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,c\,\,\,\,\,\,khi\,\,x > d\end{array} \right.\)
b) Xét tính liên tục của hàm số \(y = v\left( x \right)\) trên \(\left( { - \infty ; + \infty } \right)\)
Phương pháp giải - Xem chi tiết
a, Ta có \(n\left( x \right) = \frac{c}{{v\left( x \right)}}\)
Trong môi trường chân không thì tốc độ của ánh sáng là c
b,Hàm số liên tục trên khoảng K nếu nó liên tục tại mọi điểm thuộc K
Hàm đa thức thì liên tục trên \(\left( { - \infty ; + \infty } \right)\)
Xét tính liên tục của hàm số tại các điểm \(x = 0,x = d\)
Hàm số liên tục tại \(x = {x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}^ + } f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}^ - } f\left( x \right) = f\left( {{x_0}} \right)\) hoặc \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
Lời giải chi tiết
a, Khi \(x < 0\) hay \(x > d\) thì ánh sáng ở môi trường chân không nên \(v\left( x \right) = c\)
Khi \(0 \le x \le d\) thì \(\frac{c}{{v\left( x \right)}} = \frac{a}{{a - x}}\) vì \(n\left( x \right) = \frac{c}{{v\left( x \right)}}\), do đó \(\frac{{v\left( x \right)}}{c} = \frac{{a - x}}{a} \Leftrightarrow v\left( x \right) = c.\frac{{a - x}}{a} = c\left( {1 - \frac{x}{a}} \right)\)
b,
Tập xác định \(D = \mathbb{R}\)
Hàm số \(y = v\left( x \right)\) là hàm đa thức nên liên tục trên các khoảng \(\left( { - \infty ;0} \right)\), \(\left( {0;d} \right)\) và \(\left( {d; + \infty } \right)\)
+ Với \(x = 0 \Rightarrow v\left( 0 \right) = c\)
\(\mathop {\lim }\limits_{x \to {0^ - }} v\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} c = c;\,\,\mathop {\lim }\limits_{x \to {0^ + }} v\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} c\left( {1 - \frac{x}{a}} \right) = c\left( {1 - \frac{0}{a}} \right) = c\)
Suy ra \(\mathop {\lim }\limits_{x \to {0^ + }} v\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} v\left( x \right) = v\left( 0 \right)\) nên hàm số \(v\left( x \right)\) liên tục tại \(x = 0\)
+ Với \(x = d \Rightarrow v\left( d \right) = c\left( {1 - \frac{d}{a}} \right)\)
\(\mathop {\lim }\limits_{x \to {d^ - }} v\left( x \right) = \mathop {\lim }\limits_{x \to {d^ - }} c\left( {1 - \frac{x}{a}} \right) = c\left( {1 - \frac{d}{a}} \right);\,\,\mathop {\lim }\limits_{x \to {d^ + }} v\left( x \right) = \mathop {\lim }\limits_{x \to {d^ + }} c = c\)
Suy ra \(\mathop {\lim }\limits_{x \to {d^ - }} v\left( x \right) \ne \,\mathop {\lim }\limits_{x \to {d^ + }} v\left( x \right)\) nên hàm số \(y = v\left( x \right)\) không liên tục tại điểm \(x = d\)
Vậy hàm số \(y = v\left( x \right)\) không liên tục trên \(\left( { - \infty ; + \infty } \right)\). Hàm số \(y = v\left( x \right)\) liên tục trên các khoảng \(\left( { - \infty ;d} \right)\) và \(\left( {d; + \infty } \right)\)
Bài 3.13 trang 79 SGK Toán 11 tập 1 thuộc chương trình học về vectơ trong không gian. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản sau:
Bài 3.13 thường yêu cầu học sinh chứng minh một đẳng thức vectơ hoặc tìm một vectơ thỏa mãn một điều kiện nào đó. Để giải bài toán này, cần:
(Giả sử bài toán yêu cầu chứng minh đẳng thức vectơ A = B, với A và B là các biểu thức vectơ)
Bước 1: Chọn hệ tọa độ Oxy.
Bước 2: Giả sử các điểm có tọa độ như sau: O(0;0), A(xA; yA), B(xB; yB), C(xC; yC).
Bước 3: Biểu diễn các vectơ theo tọa độ:
Bước 4: Tính toán và biến đổi các vectơ để chứng minh đẳng thức A = B.
Ví dụ: Nếu A = OA + OB và B = OC, ta cần chứng minh OA + OB = OC. Điều này tương đương với việc chứng minh (xA + xB; yA + yB) = (xC; yC). Từ đó suy ra xA + xB = xC và yA + yB = yC.
Ngoài bài 3.13, còn rất nhiều bài tập tương tự liên quan đến vectơ trong không gian. Các bài tập này thường yêu cầu học sinh:
Để giải các bài tập này, học sinh cần nắm vững các kiến thức cơ bản về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học. Ngoài ra, cần luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau và rèn luyện kỹ năng giải toán.
Để học tốt môn Toán 11, học sinh có thể tham khảo các tài liệu sau:
Giaitoan.edu.vn luôn đồng hành cùng học sinh trong quá trình học tập môn Toán. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu và phương pháp giải bài tập hiệu quả, giúp học sinh nắm vững kiến thức và đạt kết quả tốt nhất.
Hy vọng với lời giải chi tiết và phương pháp giải bài tập Bài 3.13 trang 79 SGK Toán 11 tập 1, các em học sinh sẽ tự tin hơn trong việc học tập môn Toán.