Bài 4.34 trang 124 SGK Toán 11 tập 1 là một bài tập quan trọng trong chương trình học Toán 11, tập trung vào việc ứng dụng kiến thức đã học để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh vận dụng các công thức, định lý đã học để tìm ra lời giải chính xác.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 4.34 trang 124 SGK Toán 11 tập 1, giúp bạn hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác BCD và M là trung điểm của AD. Giao điểm của đường thẳng MG và mặt phẳng (ABC) là
Đề bài
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác BCD và M là trung điểm của AD. Giao điểm của đường thẳng MG và mặt phẳng (ABC) là
A. Giao điểm của MG và BC.
B. Giao điểm của MG và AC.
C. Giao điểm của MG và AB.
D. Giao điểm của MG và AN với N là trung điểm của BC.
Phương pháp giải - Xem chi tiết
Cách tìm giao điểm của đường thẳng a và mặt phẳng (P):
+ Bước 1: Chọn mặt phẳng (Q) chứa a. Tìm giao tuyến d của (P) và (Q)
+ Bước 2: Tìm giao điểm I của a và d. I chính là giao điểm của d và (P).
Lời giải chi tiết
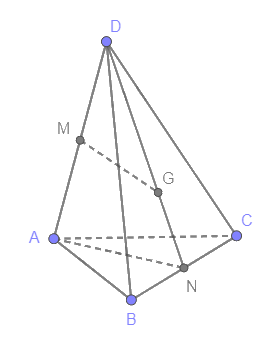
Gọi N là trung điểm của BC
(DAN) và (ABC) có giao tuyến là AN
Mà MG nằm trong (DAN) nên giao điểm của MG với (ABC) là giao điểm của MG với AN
Chọn đáp án D.
Bài 4.34 trang 124 SGK Toán 11 tập 1 thường thuộc chủ đề về đường thẳng và mặt phẳng trong không gian. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản như:
Dưới đây là phân tích chi tiết và lời giải cho Bài 4.34 trang 124 SGK Toán 11 tập 1 (giả sử bài toán cụ thể là tìm giao điểm của đường thẳng và mặt phẳng):
Đọc kỹ đề bài để xác định chính xác phương trình của đường thẳng (d) và mặt phẳng (P). Phương trình đường thẳng có thể được cho dưới dạng tham số hoặc phương trình chính tắc. Phương trình mặt phẳng thường có dạng Ax + By + Cz + D = 0.
Để xác định vị trí tương đối, ta thay tọa độ điểm thuộc đường thẳng vào phương trình mặt phẳng. Nếu kết quả là:
Nếu đường thẳng cắt mặt phẳng, ta giải hệ phương trình gồm phương trình đường thẳng và phương trình mặt phẳng để tìm tọa độ giao điểm. Có thể sử dụng phương pháp thế hoặc phương pháp cộng đại số để giải hệ phương trình.
Sau khi tìm được tọa độ giao điểm, ta kết luận về vị trí tương đối giữa đường thẳng và mặt phẳng, đồng thời đưa ra tọa độ giao điểm (nếu có).
Giả sử đường thẳng (d) có phương trình tham số: x = 1 + t, y = 2 - t, z = 3 + 2t và mặt phẳng (P) có phương trình: x + y + z - 6 = 0.
Thay tọa độ điểm thuộc đường thẳng (ví dụ, khi t = 0, ta có điểm A(1, 2, 3)) vào phương trình mặt phẳng:
1 + 2 + 3 - 6 = 0. Vậy, đường thẳng nằm trên mặt phẳng.
Nếu thay một giá trị khác của t, ví dụ t = 1, ta có điểm B(2, 1, 5). Thay vào phương trình mặt phẳng:
2 + 1 + 5 - 6 = 2 ≠ 0. Điều này mâu thuẫn với kết quả trước đó. Lỗi này cho thấy cần kiểm tra lại phương trình đường thẳng và mặt phẳng, hoặc có thể bài toán yêu cầu tìm giao điểm của đường thẳng với một mặt phẳng khác.
Để giải bài toán này một cách chính xác, cần kiểm tra lại đề bài và đảm bảo các phương trình được viết đúng. Nếu đường thẳng cắt mặt phẳng, ta sẽ giải hệ phương trình để tìm giao điểm.
Để củng cố kiến thức và kỹ năng giải Bài 4.34 trang 124 SGK Toán 11 tập 1, bạn nên luyện tập thêm các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp bạn nắm vững kiến thức và tự tin hơn khi làm bài kiểm tra.
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán. Chúc bạn học tập tốt!
Bài 4.34 trang 124 SGK Toán 11 tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về đường thẳng và mặt phẳng trong không gian. Việc nắm vững kiến thức cơ bản và luyện tập thường xuyên là chìa khóa để giải quyết thành công bài tập này.