Chào mừng các em học sinh đến với lời giải chi tiết Bài 5.16 trang 147 SGK Toán 11 tập 1. Bài học này thuộc chương trình học Toán 11 tập 1, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải bài tập Toán 11 một cách rõ ràng, dễ hiểu, giúp các em tự tin hơn trong quá trình học tập và ôn luyện.
Tuổi thọ của lốp xe ô tô được tính theo quãng đường mà lốp được sử dụng cho đến khi bắt đầu xảy ra sự cố về lốp, gọi là “quãng đường lăn bánh”. Dưới đây là bảng thống kê quãng đường lăn bánh của một số lốp xe do hãng X sản xuất:
Đề bài
Tuổi thọ của lốp xe ô tô được tính theo quãng đường mà lốp được sử dụng cho đến khi bắt đầu xảy ra sự cố về lốp, gọi là “quãng đường lăn bánh”. Dưới đây là bảng thống kê quãng đường lăn bánh của một số lốp xe do hãng X sản xuất:

a) Tính quãng đường lăn bánh trung bình của lốp xe do hãng X sản xuất.
b) Chiếm số lượng nhiều nhất là loại lốp xe có quãng đường lăn bánh xấp xỉ bao nhiêu km?
Phương pháp giải - Xem chi tiết
a) Quãng đường lăn bánh trung bình của lốp xe là đi tính trung bình của mẫu số liệu ghép nhóm.
Công thức tính trung bình là
\(\overline x = \frac{1}{N}\left( {{c_1}{n_1} + {c_2}{n_2} + ... + {c_k}{n_k}} \right)\) với \({c_k},{n_k}\) lần lượt là giá trị đại diện và tần số của nhóm thứ k
\({c_k}\) là trung bình cộng của đầu mút trái và đầu mút phải của nhóm đó.
b) Chiếm số lượng nhiều nhất chính là mốt của mẫu số liệu
Mốt tính theo công thức \({M_0} = {L_m} + \frac{a}{{a + b}}.h\)
Lời giải chi tiết
a) Để ngắn gọn, ta lập bảng sau
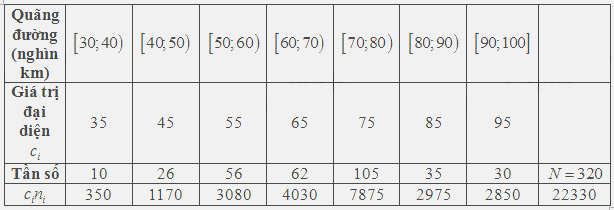
Áp dụng công thức tính trung bình ta có \(\overline x = \frac{{22330}}{{320}} = 69,78\)
Vậy quãng đường lăn bánh trung bình của lốp xe do hãng X sản xuất là 69,78 nghìn km.
b) Dựa vào bảng dữ liệu ta có nhóm chứa mốt là \(\left[ {70;80} \right)\) với tần số \(n = 105\)
Ta có \({L_m} = 70;h = 80 - 70 = 10\), \(a = 105 - 62 = 43,b = 105 - 35 = 70\)
Áp dụng công thức tính mốt ta có \({M_0} = {L_m} + \frac{a}{{a + b}}.h = 70 + \frac{{43}}{{43 + 70}}.10 \approx 73,8\)
Ta có mốt của mẫu số liệu chính là số lượng nhiều nhất là loại lốp xe có quãng đường lăn bánh xấp xỉ 73,8 nghìn km
Bài 5.16 trang 147 SGK Toán 11 tập 1 yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán liên quan đến tính đơn điệu của hàm số. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm và định lý sau:
Nội dung bài tập 5.16: (Nội dung bài tập cụ thể sẽ được trình bày chi tiết ở đây, bao gồm cả đề bài và các bước giải. Ví dụ: Cho hàm số y = x^3 - 3x^2 + 2. Hãy xét tính đơn điệu của hàm số.)
Lời giải chi tiết:
Ví dụ minh họa: (Cung cấp thêm một ví dụ tương tự để học sinh hiểu rõ hơn về cách giải bài tập.)
Lưu ý quan trọng:
Bài tập tương tự: (Liệt kê một số bài tập tương tự để học sinh luyện tập thêm.)
| STT | Bài tập |
|---|---|
| 1 | Bài 5.17 trang 147 SGK Toán 11 tập 1 |
| 2 | Bài 5.18 trang 148 SGK Toán 11 tập 1 |
Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em học sinh đã hiểu rõ cách giải Bài 5.16 trang 147 SGK Toán 11 tập 1. Hãy luyện tập thêm các bài tập tương tự để củng cố kiến thức và nâng cao kỹ năng giải toán của mình. Chúc các em học tập tốt!
Các kiến thức liên quan:
Nguồn tham khảo: