Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 1 của giaitoan.edu.vn. Ở đây, chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho tất cả các bài tập trong SGK, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Mục 1 của chương trình Toán 11 tập 1 thường tập trung vào các khái niệm cơ bản về hàm số, đồ thị hàm số và các phép biến đổi hàm số. Việc hiểu rõ những khái niệm này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong tương lai.
Cho dãy số (({u_n})) được xác định bởi ({u_n} = frac{1}{n})
Cho dãy số (\({u_n}\)) được xác định bởi \({u_n} = \frac{1}{n}\)
a, Tính giá trị của \({u_1},{u_2},{u_3},{u_4},{u_{10}}\)và biểu diễn chúng trên trục số thực dưới đây:
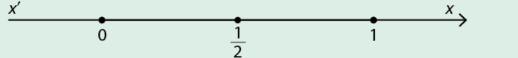
b, Khi n tăng thì khoảng cách giữa \({u_n}\) và 0 thay đổi thế nào ? Điều đó thể hiện thế nào trên trục số.
c, Bắt đầu từ số hạng thứ mấy thì khoảng cách từ \({u_n}\) đến 0 nhỏ hơn 0,01? Câu hỏi tương tự với 0,001; 0,00001.
Phương pháp giải:
a, Lần lượt thay giá trị n=1, n= 2, n=3, n=4, n= 10 vào công thức \({u_n} = \frac{1}{n}\) để được các giá trị tương ứng \({u_1},{u_2},{u_3},{u_4},{u_{10}}\).
b, Khoảng cách giữa \({u_n}\) và 0 là giá trị của \({u_n}\).
Khi n tăng thì giá trị \(\frac{1}{n}\) càng nhỏ, khoảng cách giữa \({u_n}\) và 0 càng gần nhau hơn.
Trên trục số, các giá trị n càng lớn thì khoảng cách giữa \({u_n}\) và 0 càng nhỏ.
c, 0,01=\(\frac{1}{{100}}\)= \({u_{100}}\). Với các giá trị n > 100 thì khoảng cách \({u_n}\) đến 0 nhỏ hơn 0,01.
Lời giải chi tiết:
a, Ta có: \({u_1} = \frac{1}{1} = 1\), \({u_2} = \frac{1}{2}\), \({u_3} = \frac{1}{3}\), \({u_4} = \frac{1}{4}\), \({u_{10}} = \frac{1}{{10}}\).
Biểu diễn trên trục số:

b, Khi n tăng thì \(\frac{1}{n}\) càng nhỏ do đó, khoảng cách giữa \({u_n}\) và 0 càng nhỏ khi n tăng.
c, Ta có : 0,01=\(\frac{1}{{100}}\)= \({u_{100}}\). Với các giá trị n > 100 thì khoảng cách \({u_n}\) đến 0 nhỏ hơn 0,01. Vậy bắt đầu từ số hạng thứ 101 thì khoảng cách \({u_n}\) đến 0 nhỏ hơn 0,01.
Tương tự:
0,001= \(\frac{1}{{1000}}\)=\({u_{1000}}\)
Vậy bắt đầu từ số hạng 1001 thì khoảng cách \({u_n}\) đến 0 nhỏ hơn 0,001.
0,00001=\(\frac{1}{{100000}} = {u_{100000}}\).
Vậy bắt đầu từ số hạng 100001 thì khoảng cách \({u_n}\) đến 0 nhỏ hơn 0,00001.
Cho dãy số (\({u_n}\)) với \({u_n} = {(\frac{1}{2})^n}\)
a, Viết năm số hạng đầu tiên của dãy số đã cho.
b, Khi giá trị n càng lớn thì khoảng cách giữa \({u_n}\) và 0 thay đổi thế nào?
Phương pháp giải:
a, Thay các giá trị n = 1, n = 2, n = 3, n = 4, n = 5 vào công thức \({u_n} = {(\frac{1}{2})^n}\) để được năm số hạng đầu tiên của dãy.
\({u_1} = {\left( {\frac{1}{2}} \right)^1} = \frac{1}{2}\); \({u_2} = {\left( {\frac{1}{2}} \right)^2} = \frac{1}{4}\); \({u_3} = {\left( {\frac{1}{2}} \right)^3} = \frac{1}{8}\); \({u_4} = {\left( {\frac{1}{2}} \right)^4} = \frac{1}{{16}}\); \({u_5} = {\left( {\frac{1}{2}} \right)^5} = \frac{1}{{32}}\)
b, Khi n càng tăng thì giá trị \({u_n}\) càng nhỏ. Do đó, khoảng cách \({u_n}\) và 0 càng nhỏ.
Lời giải chi tiết:
a, Ta có :
\({u_1} = {\left( {\frac{1}{2}} \right)^1} = \frac{1}{2}\); \({u_2} = {\left( {\frac{1}{2}} \right)^2} = \frac{1}{4}\); \({u_3} = {\left( {\frac{1}{2}} \right)^3} = \frac{1}{8}\); \({u_4} = {\left( {\frac{1}{2}} \right)^4} = \frac{1}{{16}}\); \({u_5} = {\left( {\frac{1}{2}} \right)^5} = \frac{1}{{32}}\)
Vậy năm số hạng đầu tiên của dãy số là: \(\frac{1}{2};\frac{1}{4};\frac{1}{8};\frac{1}{{16}};\frac{1}{{32}}\).
b, Khi n càng tăng thì khoảng cách \({u_n}\) và 0 càng nhỏ.
Cho dãy số (\({u_n}\)) với \({u_n}\)=\(\frac{{3n + 1}}{n}\). Xét dãy số (\({v_n}\)) với \({v_n} = {u_n} - 3\). Viết công thức tính số hạng tổng quát \({v_n}\)và \(\mathop {\lim }\limits_{n \to + \infty } {v_n}\).
Phương pháp giải:
Thay \({u_n}\)=\(\frac{{3n + 1}}{n}\) vào công thức \({v_n} = {u_n} - 3\) để được số hạng tổng quát của \({v_n}\).
Sử dụng phần lưu ý mục 1 là \(\mathop {\lim }\limits_{n \to + \infty } \frac{1}{n} = 0\) để tính \(\mathop {\lim }\limits_{n \to + \infty } {v_n}\).
Lời giải chi tiết:
Ta có: \({v_n} = {u_n} - 3\)= \(\frac{{3n + 1}}{n} - 3 = \frac{{3n + 1 - 3n}}{n} = \frac{1}{n}\).
Khi đó, \(\mathop {\lim }\limits_{n \to + \infty } {v_n}\)=\(\mathop {\lim }\limits_{n \to + \infty } \frac{1}{n} = 0\).
Chứng minh rằng: \(\mathop {\lim }\limits_{n \to + \infty } \frac{{1 - 4{n^2}}}{{{n^2}}} = - 4\).
Phương pháp giải:
Ta có: \(\mathop {\lim }\limits_{n \to + \infty } \left[ {\frac{{1 - 4{n^2}}}{{{n^2}}} - ( - 4)} \right] = \mathop {\lim }\limits_{n \to + \infty } \frac{1}{{{n^2}}} = 0\)
Lời giải chi tiết:
Ta có:
\(\mathop {\lim }\limits_{n \to + \infty } \left[ {\frac{{1 - 4{n^2}}}{{{n^2}}} - ( - 4)} \right]\)
=\(\mathop {\lim }\limits_{n \to + \infty } \left( {\frac{{1 - 4{n^2}}}{{{n^2}}} + 4} \right)\)
=\(\mathop {\lim }\limits_{n \to + \infty } (\frac{{1 - 4{n^2} + 4{n^2}}}{{{n^2}}})\)
\(\mathop {\lim }\limits_{n \to + \infty } \frac{1}{{{n^2}}} = 0\)
Vậy \(\mathop {\lim }\limits_{n \to + \infty } \frac{{1 - 4{n^2}}}{{{n^2}}} = - 4\).
a, Chứng minh rằng \(\mathop {\lim }\limits_{n \to + \infty } \frac{{6{n^3} + 1}}{{{n^3}}} = 6\)
b, So sánh \(\mathop {\lim }\limits_{n \to + \infty } \frac{{6{n^3} + 1}}{{{n^3}}}\) và \((\mathop {\lim }\limits_{n \to + \infty } 6 + \mathop {\lim }\limits_{n \to + \infty } \frac{1}{{{n^3}}})\).
Phương pháp giải:
a, Tính \(\mathop {\lim }\limits_{n \to + \infty } (\frac{{6{n^3} + 1}}{{{n^3}}} - 6) = \mathop {\lim }\limits_{n \to + \infty } \frac{1}{{{n^3}}} = 0\).
b, Tính \((\mathop {\lim }\limits_{n \to + \infty } 6 + \mathop {\lim }\limits_{n \to + \infty } \frac{1}{{{n^3}}})\) và sử dụng kết quả câu a để so sánh.
Lời giải chi tiết:
a, Ta có: \(\mathop {\lim }\limits_{n \to + \infty } (\frac{{6{n^3} + 1}}{{{n^3}}} - 6)\)
= \(\mathop {\lim }\limits_{n \to + \infty } \left( {\frac{{6{n^3} + 1 - 6{n^3}}}{{{n^3}}}} \right)\)
= \(\mathop {\lim }\limits_{n \to + \infty } \frac{1}{{{n^3}}} = 0\).
Vậy \(\mathop {\lim }\limits_{n \to + \infty } \frac{{6{n^3} + 1}}{{{n^3}}} = 6\).
b, Ta có: \(\mathop {\lim }\limits_{n \to + \infty } 6 = 6\) và \(\mathop {\lim }\limits_{n \to + \infty } \frac{1}{{{n^3}}} = 0\)
Do đó: \((\mathop {\lim }\limits_{n \to + \infty } 6 + \mathop {\lim }\limits_{n \to + \infty } \frac{1}{{{n^3}}})\)= 6
Vậy: \(\mathop {\lim }\limits_{n \to + \infty } \frac{{6{n^3} + 1}}{{{n^3}}}\) = \((\mathop {\lim }\limits_{n \to + \infty } 6 + \mathop {\lim }\limits_{n \to + \infty } \frac{1}{{{n^3}}})\).
Tìm \(\lim \frac{{6 - 7{n^2}}}{{2{n^3} + 9}}\) và \(\lim \frac{{{5^n} + {{2.6}^n}}}{{{6^n} + {4^n}}}\)
Phương pháp giải:
Tính \(\lim \frac{{6 - 7{n^2}}}{{2{n^3} + 9}}\) chia cả tử và mẫu cho \({n^3}\)
Tính \(\lim \frac{{{5^n} + {{2.6}^n}}}{{{6^n} + {4^n}}}\) chia cả tử và mẫu cho \({6^n}\).
Lời giải chi tiết:
Ta có: \(\frac{{6 - 7{n^2}}}{{2{n^3} + 9}} = \frac{{6.\frac{1}{{{n^3}}} - 7.\frac{1}{n}}}{{2 + 9.\frac{1}{{{n^3}}}}}\)
Vì lim 6=6, lim 7=7, lim 2= 2, lim 9=9, \(\lim \frac{1}{{{n^3}}} = 0\), \(\lim \frac{1}{n} = 0\) nên:
\(\lim (6.\frac{1}{{{n^3}}} - 7.\frac{1}{n}) = 6.0 + 7.0 = 0\) và \(\lim (2 + 9.\frac{1}{{{n^3}}}) = 2 + 9.0 = 2\)
Vậy \(\lim \frac{{6 - 7{n^2}}}{{2{n^3} + 9}}\) \( = 0\).
Ta có: \(\frac{{{5^n} + {{2.6}^n}}}{{{6^n} + {4^n}}}\) = \(\frac{{{{(\frac{5}{6})}^n} + 2}}{{1 + {{(\frac{4}{6})}^n}}} = \frac{{{{(\frac{5}{6})}^n} + 2}}{{1 + {{(\frac{2}{3})}^n}}}\)
Vì \(\lim {(\frac{5}{6})^n} = 0\); \(\lim {(\frac{2}{3})^n} = 0\); \(\lim 2 = 2\); \(\lim 1 = 1\) nên :
\(\lim \left[ {{{(\frac{5}{6})}^n} + 2} \right] = 2\)và \(\lim \left[ {1 + {{\left( {\frac{2}{3}} \right)}^n}} \right] = 1\)
Vậy \(\lim \frac{{{5^n} + {{2.6}^n}}}{{{6^n} + {4^n}}}\)= 2.
1.Chứng minh rằng dãy số (\({u_n}\)) và (\({v_n}\)) với công thức tính số hạng tổng quát lần lượt là \({u_n} = {(\frac{1}{2})^n}\) và \({v_n} = 2.{(\frac{{ - 2}}{3})^n}\) là cấp số nhân mà công bội của chúng có giá trị tuyệt đối nhỏ hơn 1.
2.Cho cấp số nhân (\({u_n}\)) có công bội q. ( \(\left| q \right| < 1\))
a, Viết công thức tính tổng \({S_n}\) của n số hạng đầu tiên của (\({u_n}\)) theo \({u_1}\) và q.
b, Nếu quy ước S=\({u_1} + {u_2} + ... + {u_n} + ... = \lim {S_n}\), hãy tính S theo \({u_1}\) và q.
Phương pháp giải:
1.Tìm công bội q của dãy số (\({u_n}\)) và (\({v_n}\)) để chứng minh là cấp số nhân
2. a, Viết công thức tính \({S_n}\) của cấp số nhân \({S_n} = \frac{{{u_{1.}}.(1 - {q^n})}}{{1 - q}}\)
b, Dựa vào lim\({q^n} = 0\), tính lim \({S_n}\).
Lời giải chi tiết:
1.Chứng minh dãy số (\({u_n}\)) là cấp số nhân
Ta có: \({u_{n + 1}} = {(\frac{1}{2})^{n + 1}}\) ; \({u_n} = {(\frac{1}{2})^n}\)
\( \Rightarrow \frac{{{u_{n + 1}}}}{{{u_n}}} = \frac{{{{(\frac{1}{2})}^{n + 1}}}}{{{{(\frac{1}{2})}^n}}} = \frac{1}{2}\)
Vậy dãy số (\({u_n}\)) là cấp số nhân với công bội q=\(\frac{1}{2}\).
Chứng minh dãy số (\({v_n}\)) là cấp số nhân
Ta có: \({v_{n + 1}} = 2.{(\frac{{ - 2}}{3})^{n + 1}}\); \({v_n} = 2.{(\frac{{ - 2}}{3})^n}\)
\( \Rightarrow \frac{{{v_{n + 1}}}}{{{v_n}}} = \frac{{2.{{(\frac{{ - 2}}{3})}^{n + 1}}}}{{2.{{(\frac{{ - 2}}{3})}^n}}} = \frac{{ - 2}}{3}\)
Vậy dãy số (\({v_n}\)) là cấp số nhân với công bội \(q = \frac{{ - 2}}{3}\).
2. a, Tổng \({S_n}\) của n số hạng đầu tiên của (\({u_n}\)) theo \({u_1}\) và q là: \({S_n} = \frac{{{u_{1.}}.(1 - {q^n})}}{{1 - q}}\)
b, S=\({u_1} + {u_2} + ... + {u_n} + ... = \lim {S_n}\)= \(\lim \frac{{{u_1}.(1 - {q^n})}}{{1 - q}}\)
Ta có lim \({q^n} = 0\)( với \(\left| q \right| < 1\)) \( \Rightarrow \lim (1 - {q^n}) = 1\), lim \({u_1} = {u_1}\), lim (1-q)=1-q
lim\({S_n} = \)\(\frac{{1.{u_1}}}{{1 - q}} = \frac{{{u_1}}}{{1 - q}}\).
Tính tổng cấp số nhân lùi vô hạn S= \(1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^n}}} + ...\)
Phương pháp giải:
S là tổng của cấp số nhân lùi vô hạn với công bội \(q = \frac{1}{2}\) và \({u_1} = 1\) .Áp dụng công thức S=\(\frac{{{u_1}}}{{1 - q}}\) để tính tổng.
Lời giải chi tiết:
Ta có S là tổng của cấp số nhân lùi vô hạn với công bội \(q = \frac{1}{2}\) và \({u_1} = 1\).
S=\(\frac{{{u_1}}}{{1 - q}}\)=\(\frac{1}{{1 - \frac{1}{2}}} = \frac{1}{{\frac{1}{2}}} = 2\).
Mục 1 của SGK Toán 11 tập 1 thường xoay quanh các khái niệm về hàm số bậc hai, bao gồm định nghĩa, các dạng biểu diễn, tính chất và ứng dụng. Việc nắm vững kiến thức này là vô cùng quan trọng để xây dựng nền tảng vững chắc cho các chương trình học toán ở các lớp trên.
Các bài tập trên trang 59 thường yêu cầu học sinh xác định các hệ số a, b, c của hàm số bậc hai, xác định tập xác định và tập giá trị của hàm số. Đồng thời, học sinh cần phân biệt được các dạng hàm số bậc hai khác nhau.
Trang 60 tập trung vào việc vẽ đồ thị hàm số bậc hai, xác định tọa độ đỉnh, trục đối xứng và giao điểm với các trục tọa độ. Việc hiểu rõ hình dạng đồ thị hàm số bậc hai giúp học sinh dự đoán được tính chất của hàm số và giải quyết các bài toán liên quan.
Các bài tập trên trang 61 yêu cầu học sinh xác định khoảng đồng biến, nghịch biến, giá trị lớn nhất, giá trị nhỏ nhất của hàm số bậc hai. Đây là những kiến thức quan trọng để giải quyết các bài toán tối ưu hóa và ứng dụng thực tế.
Trang 62 là nơi tổng hợp các bài tập vận dụng kiến thức đã học để giải quyết các bài toán phức tạp hơn. Các bài tập này thường đòi hỏi học sinh phải kết hợp nhiều kiến thức khác nhau và có khả năng tư duy logic.
Bài tập: Tìm tọa độ đỉnh của parabol y = x2 - 4x + 3.
Lời giải:
Khi giải bài tập về hàm số bậc hai, cần chú ý đến điều kiện xác định của hàm số và các trường hợp đặc biệt. Đồng thời, hãy rèn luyện kỹ năng vẽ đồ thị hàm số để có thể giải quyết các bài toán một cách nhanh chóng và chính xác.
Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh đã có thể tự tin giải quyết các bài tập trong mục 1 trang 59, 60, 61, 62 SGK Toán 11 tập 1. Chúc các em học tập tốt và đạt kết quả cao!