Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 1 của giaitoan.edu.vn. Ở đây, chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho tất cả các bài tập trong sách giáo khoa, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Mục 2 của chương trình Toán 11 tập 1 thường xoay quanh các chủ đề về phép vectơ, các phép toán vectơ, và ứng dụng của vectơ trong hình học.
Cho hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\). Biết rằng hai đường thẳng a và b nằm trong \(\left( \alpha \right)\) sao cho \(a\,{\rm{//}}\left( \beta \right)\) và \(b\,{\rm{//}}\left( \beta \right)\).
Cho hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\). Biết rằng hai đường thẳng a và b nằm trong \(\left( \alpha \right)\) sao cho \(a\,{\rm{//}}\left( \beta \right)\) và \(b\,{\rm{//}}\left( \beta \right)\).
a) Vì sao \(\left( \alpha \right)\) và \(\left( \beta \right)\) là hai mặt phẳng phân biệt?
b) Nếu \(\left( \alpha \right)\) cắt \(\left( \beta \right)\) theo giao tuyến c thì c có song song với a và b hay không?
c) Nếu a cắt b tại M thì \(\left( \alpha \right)\) và \(\left( \beta \right)\) có thể có điểm chung hay không ?
Phương pháp giải:
a) Hai mặt phẳng phân biệt là hai mặt phẳng không trùng nhau.
b) Cho a // (P). Nếu (Q) chứa a và (Q) cắt (P) theo giao tuyến b thì a // b.
c) Chứng minh phản chứng (Giả sử \(\left( \alpha \right)\) và \(\left( \beta \right)\) có điểm chung).
Lời giải chi tiết:
a) Nếu \(\left( \alpha \right)\) và \(\left( \beta \right)\) trùng nhau thì a, b song song với \(\left( \alpha \right)\)
Mà a, b nằm trong \(\left( \alpha \right)\) (Mâu thuẫn)
Vậy \(\left( \alpha \right)\) và \(\left( \beta \right)\) là hai mặt phẳng phân biệt.
b) \(a\,{\rm{//}}\left( \beta \right)\), \(b\,{\rm{//}}\left( \beta \right)\)
Mà \(\left( \alpha \right)\) cắt \(\left( \beta \right)\) theo giao tuyến c nên a // c, b // c.
c) Giả sử \(\left( \alpha \right)\) và \(\left( \beta \right)\) có điểm chung. Vì \(\left( \alpha \right)\) cắt \(\left( \beta \right)\) là 2 mặt phẳng phân biệt nên \(\left( \alpha \right)\) cắt \(\left( \beta \right)\)
Theo phần b, suy ra a // c // b (Mâu thuẫn)
Vậy nếu a cắt b tại M thì \(\left( \alpha \right)\) cắt \(\left( \beta \right)\) không có điểm chung.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm của SA, SB, SC. Chứng minh rằng mặt phẳng (MNP) song song với mặt phẳng (ABCD).
Phương pháp giải:
Nếu mặt phẳng (P) chứa 2 đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng (Q) thì (P) song song với (Q).
Lời giải chi tiết:
Xét tam giác SAB có M, N lần lượt là trung điểm của SA, SB nên MN // AB. Suy ra MN // (ABCD).
Xét tam giác SBC có N, P lần lượt là trung điểm của SB, SC nên NP // BC. Suy ra NP // (ABCD).
Vậy (MNP) // (ABCD).
Cho điểm A nằm ngoài một mặt phẳng \(\left( \beta \right)\). Trong \(\left( \beta \right)\), lấy hai đường thẳng cắt nhau a và b. Vẽ các đường thẳng \({d_1}\), \({d_2}\) qua A và lần lượt song song với a, b. Gọi \(\left( \alpha \right)\) là mặt phẳng xác định bởi \({d_1}\) và \({d_2}\). Mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) có điểm chung không? Vì sao?
Phương pháp giải:
Nếu mặt phẳng (P) chứa 2 đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng (Q) thì (P) song song với (Q).
Lời giải chi tiết:
\(\begin{array}{l}\left\{ \begin{array}{l}{d_1}\,{\rm{//}}\,a\\a \subset \left( \beta \right)\end{array} \right. \Rightarrow {d_1}\,{\rm{//}}\,\left( \beta \right)\\\left\{ \begin{array}{l}{d_2}\,{\rm{//}}\,b\\b \subset \left( \beta \right)\end{array} \right. \Rightarrow {d_2}\,{\rm{//}}\,\left( \beta \right)\end{array}\)
Mặt phẳng \(\left( \alpha \right)\) chứa \({d_1}\), \({d_2}\) cắt nhau tại A và cùng song song với \(\left( \beta \right)\) nên \(\left( \alpha \right)\) song song với \(\left( \beta \right)\).
Vậy mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) không điểm chung.
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Lấy M là trung điểm của đoạn AD. Gọi \(\left( \alpha \right)\) là mặt phẳng qua M và song song với mặt phẳng (SAC). Xác định giao tuyến của \(\left( \alpha \right)\) với các mặt của hình chóp đã cho.
Phương pháp giải:
Kẻ 2 đường thẳng đi qua M và song song với 2 đường thẳng trong (SAC).
Lời giải chi tiết:

Trong tam giác SAD, vẽ đường thẳng đi qua M, song song với SA, cắt SD tại E (tức ME là đường trung bình của tam giác SAD), suy ra ME // (SAC) (1).
Trong tam giác ACD, vẽ đường thẳng đi qua M, song song với AC, cắt CD tại F (tức MF là đường trung bình của tam giác ACD), suy ra MF // (SAC) (2).
Từ (1) và (2) suy ra (ME, MF) // (SAC), do đó (MEF) là \(\left( \alpha \right)\).
\(\begin{array}{l}\left( {MEF} \right) \cap \left( {ABCD} \right) = MF\\\left( {MEF} \right) \cap \left( {SAD} \right) = ME\\\left( {MEF} \right) \cap \left( {SCD} \right) = EF\end{array}\)
Cho hình chóp S.ABC. Gọi M là trung điểm của SA. Một đường thẳng d đi qua M và song song với mặt phẳng (ABC) nhưng không song song với BC. Xác định giao điểm của d với mặt phẳng (SBC).
Phương pháp giải:
Kẻ đường thẳng đi qua M và song song với một đường thẳng nằm trong (SBC) khác BC.
Lời giải chi tiết:

Trong tam giác SAB, vẽ đường thẳng d đi qua M và song song với AB, cắt SB tại D (tức MD là đường trung bình của tam giác SAB), suy ra MD // (ABC).
Vậy giao điểm của d với (ABC) là D.
Cho mặt phẳng \(\left( \gamma \right)\) cắt hai mặt phẳng song song \(\left( \alpha \right)\) và \(\left( \beta \right)\) lần lượt theo hai giao tuyến a và b. Hỏi a và b có điểm chung hay không? Vì sao?
Phương pháp giải:
Hai đường thẳng lần lượt nằm trong 2 mặt phẳng song song thì song song hoặc chéo nhau.
Lời giải chi tiết:
Đường thẳng a, b lần lượt nằm trong 2 mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) song song với nhau nên a và b song song hoặc chéo nhau.
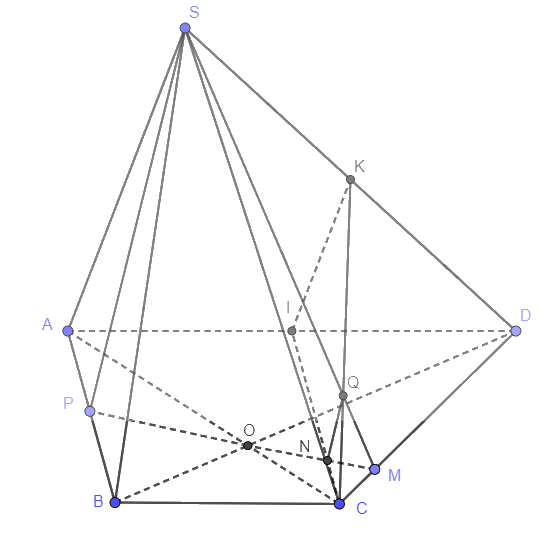
Cho hình chóp S.ABCD có đáy là hình thang ABCD với đáy lớn AD = 2BC. Gọi I, K lần lượt là trung điểm của AD và SD.
a) Chứng minh rằng (SAB) // (CIK).
b) Gọi O là giao điểm của hai đường chéo AC, BD. Lấy M là điểm bất kì trên đoạn CD, đường thẳng OM cắt CI, AB lần lượt tại N, P và SM cắt CK tại Q. Chứng minh rằng SP // NQ.
Phương pháp giải:
a) Nếu mặt phẳng (P) chứa 2 đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng (Q) thì (P) song song với (Q).
b) Cho 2 mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau.
Lời giải chi tiết:

a) Xét tam giác SAD có I, K lần lượt là trung điểm của AD, SD nên IK // SA.
Ta có có AD // BC (ABCD là hình thang), AI = BC nên ABCI là hình bình hành. Suy ra IC // AB.
Vậy (CIK) // (SAB).
b)
\(\begin{array}{l}\left( {SAB} \right) \cap \left( {SPM} \right) = SP\\\left( {CIK} \right) \cap \left( {SPM} \right) = NQ\end{array}\)
Mà (SAB) // (CIK) (cmt) nên SP // NQ.
Mục 2 trong SGK Toán 11 tập 1 tập trung vào việc củng cố và mở rộng kiến thức về vectơ, bao gồm các phép toán cơ bản như cộng, trừ, nhân với một số thực, và tích vô hướng của hai vectơ. Việc nắm vững các khái niệm và kỹ năng này là nền tảng quan trọng để giải quyết các bài toán hình học và vật lý ở các lớp trên.
Các bài tập trên trang 107 thường yêu cầu học sinh thực hiện các phép cộng và trừ vectơ dựa trên tọa độ của chúng. Để giải quyết các bài tập này, học sinh cần nắm vững quy tắc cộng và trừ vectơ: cộng (hoặc trừ) các hoành độ tương ứng, cộng (hoặc trừ) các tung độ tương ứng.
Trang 108 tập trung vào phép nhân vectơ với một số thực. Quy tắc nhân vectơ với một số thực là nhân mỗi thành phần của vectơ với số thực đó. Các bài tập thường yêu cầu học sinh tính tích của một vectơ với một số thực, hoặc chứng minh các đẳng thức liên quan đến phép nhân vectơ với một số thực.
Tích vô hướng của hai vectơ là một khái niệm quan trọng trong hình học vectơ. Nó được sử dụng để tính góc giữa hai vectơ, kiểm tra tính vuông góc của hai vectơ, và tính độ dài của một vectơ. Các bài tập trên trang 109 thường yêu cầu học sinh tính tích vô hướng của hai vectơ, hoặc sử dụng tích vô hướng để giải quyết các bài toán hình học.
Công thức tính tích vô hướng của hai vectơ a = (x1, y1) và b = (x2, y2) là: a.b = x1*x2 + y1*y2.
Trang 110 thường chứa các bài tập tổng hợp, yêu cầu học sinh vận dụng kiến thức về tất cả các phép toán vectơ đã học để giải quyết các bài toán phức tạp hơn. Các bài tập này thường liên quan đến việc chứng minh các đẳng thức hình học, tìm tọa độ của các điểm, hoặc giải các bài toán ứng dụng.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, và được trình bày một cách khoa học. Chúng tôi luôn cập nhật lời giải mới nhất và đảm bảo tính chính xác của các bài giải. Ngoài ra, chúng tôi còn cung cấp nhiều tài liệu học tập hữu ích khác, giúp các em học toán hiệu quả hơn.
Hy vọng rằng với những lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh sẽ tự tin hơn trong việc giải các bài tập mục 2 trang 107, 108, 109, 110 SGK Toán 11 tập 1. Chúc các em học tập tốt!