Bài 8.11 trang 63 SGK Toán 11 tập 2 là một bài tập quan trọng trong chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng giải bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, cùng với các phương pháp giải nhanh chóng và hiệu quả, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a
Đề bài
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S trên (ABC) trùng với trung điểm H của cạnh BC và SBC là tam giác đều. Tính số đo của góc giữa SA và (ABC).
Phương pháp giải - Xem chi tiết
Chứng minh \(AH\) là hình chiếu vuông góc của \(SA\) trên \(\left( {ABC} \right)\) từ đó suy ra góc cần tìm là góc \(\widehat {SAH}\)
Dựa vào đường trung tuyến của tam giác đều để tính cạnh \(AH,SH\)
Sử dụng tỉ số lượng giác: \(\tan \alpha \) để tính số đo góc
Lời giải chi tiết
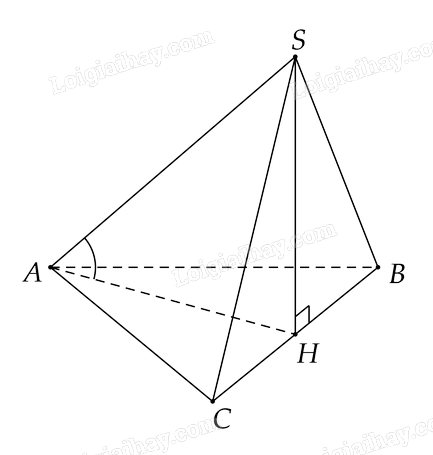
Vì hình chiếu vuông góc của \(S\) trên \(\left( {ABC} \right)\) là trung điểm \(H\) của \(BC\) nên \(SH \bot \left( {ABC} \right)\)
Vì \(SH \bot \left( {ABC} \right)\) nên \(AH\) là hình chiếu vuông góc của \(SA\) trên \(\left( {ABC} \right)\)
Vậy góc giữa \(SA\) và \(\left( {ABC} \right)\) là góc giữa \(SA\) và \(AH\), góc giữa \(SA\) và \(AH\) là góc \(\widehat {SAH}\)
Vì \(\Delta ABC\) là tam giác đều cạnh \(a\) suy ra đường trung tuyến \(AH\) nên \(AH = \frac{{a\sqrt 3 }}{2}\)
Vì \(\Delta SBC\) là tam giác đều có cạnh \(BC = a\) suy ra đường trung tuyến \(SH = \frac{{a\sqrt 3 }}{2}\)
Xét \(\Delta SAH\) vuông tại \(A\) có \(\tan \widehat {SAH} = \frac{{SH}}{{AH}} = \frac{{a\sqrt 3 }}{2}:\frac{{a\sqrt 3 }}{2} = 1\)\( \Rightarrow \widehat {SAH} = {45^o}\)
Bài 8.11 trang 63 SGK Toán 11 tập 2 yêu cầu học sinh giải một bài toán thực tế liên quan đến việc tối ưu hóa một đại lượng nào đó bằng cách sử dụng đạo hàm. Để giải bài toán này, học sinh cần nắm vững các kiến thức về đạo hàm, điều kiện cần và đủ để hàm số đạt cực trị, và các phương pháp giải bài toán tối ưu hóa.
Trước khi bắt đầu giải bài toán, học sinh cần đọc kỹ đề bài để hiểu rõ yêu cầu của bài toán. Xác định các đại lượng cần tìm, các điều kiện ràng buộc, và mục tiêu cần đạt được. Trong bài 8.11, học sinh cần xác định hàm số cần khảo sát, tìm tập xác định của hàm số, tính đạo hàm, và tìm các điểm cực trị của hàm số.
Để giải bài toán tối ưu hóa, học sinh có thể sử dụng các phương pháp sau:
(Nội dung giải chi tiết bài toán sẽ được trình bày tại đây, bao gồm các bước giải cụ thể, các công thức sử dụng, và các kết luận rút ra. Ví dụ:)
Giả sử bài toán yêu cầu tìm giá trị lớn nhất của diện tích hình chữ nhật nội tiếp trong nửa đường tròn bán kính R. Gọi x là độ dài một cạnh của hình chữ nhật. Khi đó, cạnh còn lại của hình chữ nhật là y = √(R² - x²). Diện tích hình chữ nhật là S = xy = x√(R² - x²). Để tìm giá trị lớn nhất của S, ta tính đạo hàm S' theo x và giải phương trình S' = 0. Sau khi giải phương trình, ta tìm được x = R/√2. Thay x = R/√2 vào công thức tính S, ta được Smax = R²/2. Vậy, diện tích lớn nhất của hình chữ nhật nội tiếp trong nửa đường tròn bán kính R là R²/2.
Khi giải bài toán tối ưu hóa, học sinh cần lưu ý các điểm sau:
Để củng cố kiến thức và kỹ năng giải bài toán tối ưu hóa, học sinh có thể làm thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp học sinh nắm vững kiến thức và tự tin giải các bài toán khó hơn.
Đạo hàm có rất nhiều ứng dụng trong thực tế, chẳng hạn như trong việc tính vận tốc, gia tốc, tối ưu hóa chi phí, lợi nhuận, và thiết kế các sản phẩm kỹ thuật. Việc hiểu rõ về đạo hàm và ứng dụng của đạo hàm sẽ giúp học sinh có thể giải quyết các vấn đề thực tế một cách hiệu quả.
Bài 8.11 trang 63 SGK Toán 11 tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán tối ưu hóa bằng cách sử dụng đạo hàm. Bằng cách nắm vững kiến thức và phương pháp giải bài toán, học sinh có thể tự tin giải các bài tập tương tự và ứng dụng kiến thức vào thực tế.