Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11 tập 2. Mục 3 của chương trình Toán 11 tập 2 thường xoay quanh các kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi sự tư duy và vận dụng kiến thức. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn bộ giải chi tiết, giúp bạn nắm vững kiến thức và tự tin giải quyết mọi bài tập.
Xét hàm số \(y = \sin x\)
Xét hàm số \(y = \sin x\)
Cho biết \(\mathop {\lim }\limits_{x \to 0} \frac{{\sin x}}{x} = 1\). Bằng định nghĩa hãy tính đạo hàm của hàm số \(y = \sin x\) tại điểm \({x_0}\) bất kì.
Phương pháp giải:
Sử dụng định nghĩa để tính đạo hàm của hàm số
Lời giải chi tiết:
Với mọi \({x_0} \in R\) ta có:
\(\mathop {\lim }\limits_{x \to {x_0}} \frac{{{\mathop{\rm s}\nolimits} {\rm{inx}} - {\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{x}}_0}}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{2.\cos \frac{{x + {x_0}}}{2}.\sin \frac{{x - {x_0}}}{2}}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \cos \frac{{x + {x_0}}}{2}.\mathop {\lim }\limits_{x \to {x_0}} \frac{{\sin \frac{{x - {x_0}}}{2}}}{{\frac{{x - {x_0}}}{2}}} = \cos {x_0}\)
Vậy \({y'} = \cos x\)
a, Từ công thức \(\cos x = \sin (\frac{\pi }{2} - x)\) và quy tắc tính đạo hàm của hàm hợp, chứng minh rằng: \({(\cos x)'} = - \sin x\)
b, Từ các công thức \(\tan x = \frac{{{\mathop{\rm s}\nolimits} {\rm{inx}}}}{{\cos x}}\), \(\cot x = \frac{{\cos x}}{{{\mathop{\rm s}\nolimits} {\rm{inx}}}}\) và các quy tắc tính đạo hàm của thương, chứng minh rằng: \({(\tan x)'} = \frac{1}{{{{\cos }^2}x}}\) và \({(\cot x)'} = \frac{{ - 1}}{{{{\sin }^2}x}}\)
Phương pháp giải:
a, Sử dụng hàm hợp và \({({\mathop{\rm s}\nolimits} {\rm{inx}})'} = \cos x\)
b, Sử dụng quy tắc \({(\frac{u}{v})'} = \frac{{{u'}.v - u.{v'}}}{{{v^2}}}\)
Lời giải chi tiết:
a, Ta có: \({(\cos x)'} = {{\rm{[}}\sin (\frac{\pi }{2} - x){\rm{]}}'} = \cos (\frac{\pi }{2} - x).{(\frac{\pi }{2} - x)'} = - \cos (\frac{\pi }{2} - x) = - {\mathop{\rm s}\nolimits} {\rm{inx}}\)
b, Ta có: \({(\tan x)'} = \frac{{{{({\mathop{\rm s}\nolimits} {\rm{inx)}}}'}.\cos x - {\mathop{\rm s}\nolimits} {\rm{inx}}.{{(\cos x)}'}}}{{{{\cos }^2}x}} = \frac{{{{\cos }^2}x + {{\sin }^2}x}}{{{{\cos }^2}x}} = \frac{1}{{{{\cos }^2}x}}\)
\({(\cot x)'} = \frac{{{{(\cos x)}'}.{\mathop{\rm s}\nolimits} {\rm{inx}} - \cos x.{{({\mathop{\rm s}\nolimits} {\rm{inx}})}'}}}{{{\mathop{\rm s}\nolimits} {\rm{i}}{{\rm{n}}^2}{\rm{x}}}} = \frac{{ - ({{\sin }^2}x + {{\cos }^2}x)}}{{{{\sin }^2}x}} = \frac{{ - 1}}{{{{\sin }^2}x}}\)
Tính đạo hàm các hàm số sau:
a, \(y = 3\cot x - \frac{{\tan x}}{2} + 1\)
b, \(y = \frac{{{\mathop{\rm s}\nolimits} {\rm{inx}}}}{x}\)
Phương pháp giải:
Sử dụng các quy tắc :\({(\tan x)'} = \frac{1}{{{{\cos }^2}x}}\) ,\({(\cot x)'} = \frac{{ - 1}}{{{{\sin }^2}x}}\), \({({\mathop{\rm s}\nolimits} {\rm{inx}})'} = \cos x\)
Lời giải chi tiết:
a, \({y'} = {(3\cot x - \frac{{\tan x}}{2} + 1)'} = \frac{{ - 3}}{{{{\sin }^2}x}} - \frac{1}{{2{{\cos }^2}x}}\)
b, \({y'} = {(\frac{{{\mathop{\rm s}\nolimits} {\rm{inx}}}}{x})'} = \frac{{{{({\mathop{\rm s}\nolimits} {\rm{inx}})}'}.x - {x'}.{\mathop{\rm s}\nolimits} {\rm{inx}}}}{{{x^2}}} = \frac{{\cos x.x - {\mathop{\rm s}\nolimits} {\rm{inx}}}}{{{x^2}}}\)
Phương trình chuyển động của một con lắc lò xo quanh vị trí cân bằng O là \(x = 4.\cos 2t\), trong đó t được tính bằng giây và x được tính bằng cm. Biết rằng vận tốc của con lắc ở thời điểm t được tính bởi \(v(t) = {x'}(t)\)
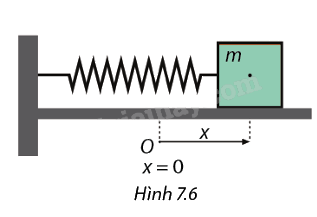
a, Tính vận tốc của con lắc tại thời điểm \(t = \frac{{7\pi }}{{12}}\)
b, Tìm thời điểm đầu tiên con lắc đạt vận tốc lớn nhất
Phương pháp giải:
a, Tính \(v(t) = {x'}(t)\) và thay \(t = \frac{{7\pi }}{{12}}\)
b, Từ câu a tìm thời điểm con lắc đạt vận tốc lớn nhất
Lời giải chi tiết:
a, Ta có: \(v(t) = {x'}(t) = {(4.\cos 2t)'} = 4.2. - \sin 2t = - 8.\sin 2t\)
Thay \(t = \frac{{7\pi }}{{12}}\) ta được: \(v(\frac{{7\pi }}{{12}}) = - 8\sin \left( {2.\frac{{7\pi }}{{12}}} \right) = - 8.\sin \left( {\frac{{7\pi }}{6}} \right) = 4\) (cm/s)
b, Ta có: \( - 1 \le \sin 2t \le 1\)\( \Rightarrow - 8 \le - 8\sin 2t \le 8\)
Con lắc đạt vận tốc lớn nhất khi sin 2t=-1\( \Rightarrow 2t = \frac{{3\pi }}{2} \Rightarrow t = \frac{{3\pi }}{4}\)
Xét hàm số \(y = {e^x}\)
Cho biết \(\mathop {\lim }\limits_{x \to 0} \frac{{{e^x} - 1}}{x} = 1.\)Bằng định nghĩa tính đạo hàm của hàm số \(y = {e^x}\) tại điểm \({x_0}\) bất kì.
Phương pháp giải:
Sử dụng định nghĩa để tính đạo hàm
Lời giải chi tiết:
Với mọi \({x_0} \in R\) ta có:
\(\mathop {\lim }\limits_{x \to {x_0}} \frac{{{e^x} - {e^{{x_0}}}}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{({e^{x - {x_0}}} - 1){e^{{x_0}}}}}{{x - {x_0}}} = {e^{{x_0}}}\)
Vậy \({y'} = {e^x}\).
a, Từ công thức \({a^x} = {e^{x\ln a}}\) và quy tắc tính đạo hàm của hàm hợp, hãy tìm công thức tính đạo hàm của hàm số \(y = {a^x}\)
b, Từ công thức \({\log _a}x = \frac{{\ln x}}{{\ln a}}\) và các quy tắc tính đạo hàm đã biết, hãy tìm công thức tính đạo hàm của hàm số \(y = {\log _a}x\)
Phương pháp giải:
a, Sử dụng công thức \({({e^x})'} = {e^x}\)
b, Sử dụng quy tắc \({(\frac{u}{v})'} = \frac{{{u'}.v - u.{v'}}}{{{v^2}}}\)
Lời giải chi tiết:
a, Ta có: \({({a^x})'} = {({e^{x\ln a}})'} = {(x.\ln a)'}.{e^{x.\ln a}} = \ln a.{e^{x.\ln a}} = \ln a.{a^x}\)
b, Ta có: \({({\log _a}x)'} = {(\frac{{\ln x}}{{\ln a}})'} = \frac{{{{(\ln x)}'}.\ln a - \ln x.{{(\ln a)}'}}}{{{{\ln }^2}a}} = \frac{{\frac{1}{x}.\ln a}}{{{{\ln }^2}a}} = \frac{1}{{x.\ln a}}\)
Tính đạo hàm các hàm số sau:
a,\(y = {4^{{\mathop{\rm s}\nolimits} {\rm{inx}} + \cos x}}\)
b, \(y = \ln (1 + \sqrt x )\)
c, \(y = \frac{{\ln x}}{x}\)
Phương pháp giải:
a, Sử dụng đạo hàm hàm hợp \({y'} = {({a^u})'} = {u'}{a^u}.\ln a\)
b, Sử dụng đạo hàm hàm hợp \({y'} = {(\ln u)'} = \frac{{{u'}}}{u}\)
c, Sử dụng quy tắc \({(\frac{u}{v})'} = \frac{{{u'}.v - u.{v'}}}{{{v^2}}}\)
Lời giải chi tiết:
a, Ta có: \(\begin{array}{l}{y'} = {({4^{{\mathop{\rm s}\nolimits} {\rm{inx}} + \cos x}})'} = {({\mathop{\rm s}\nolimits} {\rm{inx}} + \cos x)'}{.4^{{\mathop{\rm s}\nolimits} {\rm{inx}} + \cos x}}.\ln 4\\ = (\cos x - \sin x){.4^{{\mathop{\rm s}\nolimits} {\rm{inx}} + \cos x}}.\ln 4\end{array}\)
b, Ta có: \({y'} = {{\rm{[}}\ln (1 + \sqrt x ){\rm{]}}'} = \frac{{{{(1 + \sqrt x )}'}}}{{1 + \sqrt x }} = \frac{1}{{2\sqrt x .(1 + \sqrt x )}}\)
c, Ta có: \({y'} = {(\frac{{\ln x}}{x})'} = \frac{{{{(\ln x)}'}.x - {x'}.\ln x}}{{{x^2}}} = \frac{{1 - \ln x}}{{{x^2}}}\)
Nồng độ C (\(\eta g/l\)) của loại thuốc A một người uống vào sau t giờ cho bởi hàm số sau \(C(t) = 6,2.{t^4}.{e^{ - 0,5t}}\). Biết rằng nồng độ C sẽ tăng lên trong 8 giờ đầu tiên và tốc độ tăng của nồng độ C tại thời điểm t được tính bởi công thức \({C'}(t)\):
a, Tính tốc độ tăng nồng độ của thuốc A tại thời điểm \({t_0} = 1\)
b, Trong hai thời điểm \({t_0} = 1\) và \({t_1} = 5\) thời điểm nào nồng độ thuốc A tăng nhanh hơn?
Phương pháp giải:
a, Tính đạo hàm của hàm số C(t) và thay \({t_0} = 1\)
b, Thay \({t_0} = 1\) và \({t_1} = 5\) và so sánh
Lời giải chi tiết:
a, Ta có:
\(\begin{array}{l}{C'}(t) = {(6,2.{t^4}.{e^{ - 0,5t}})'} = 6,2.(4{t^3}.{e^{ - 0,5t}} + {t^4}.( - 0,5).{e^{ - 0,5t}})\\ = 24,8{t^3}.{e^{ - 0,5t}} - 3,1.{t^4}.{e^{ - 0,5t}}\end{array}\)
\({C'}(1) = 24,{8.1^3}.{e^{ - 0,5}} - 3,{1.1^4}.{e^{ - 0,5}} = 21,7.{e^{ - 0,5}} \approx 13,1617\)
b, \({C'}(5) = 24,{8.5^3}.{e^{ - 0,5.5}} - 3,{1.5^4}.{e^{ - 0,5.5}} \approx 95,4238\)
Vậy nồng độ tại thời điểm t=5 giây có nồng độ cao hơn.
Mục 3 của SGK Toán 11 tập 2 tập trung vào việc củng cố và mở rộng kiến thức về đạo hàm, đặc biệt là các ứng dụng của đạo hàm trong việc khảo sát hàm số. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các công thức đạo hàm, quy tắc tính đạo hàm, và các phương pháp tìm cực trị, điểm uốn của hàm số.
Để giúp các bạn học sinh giải quyết các bài tập trong mục 3 một cách hiệu quả, giaitoan.edu.vn xin trình bày hướng dẫn giải chi tiết cho từng bài tập:
Bài tập này yêu cầu tính đạo hàm của các hàm số cho trước. Để giải bài tập này, bạn cần áp dụng các quy tắc tính đạo hàm đã học. Ví dụ, để tính đạo hàm của hàm số y = x2 + 3x - 2, bạn cần sử dụng quy tắc đạo hàm của tổng và quy tắc đạo hàm của lũy thừa. Kết quả là y' = 2x + 3.
Bài tập này yêu cầu tìm cực trị của hàm số. Để giải bài tập này, bạn cần tìm các điểm mà đạo hàm bằng 0 hoặc không tồn tại, sau đó xét dấu đạo hàm để xác định xem các điểm đó là điểm cực đại hay cực tiểu.
Bài tập này yêu cầu khảo sát hàm số. Để giải bài tập này, bạn cần xác định tập xác định, các điểm gián đoạn, các điểm cực trị, khoảng đơn điệu, giới hạn và vẽ đồ thị hàm số.
Bài tập này thường là một bài toán thực tế ứng dụng đạo hàm để giải quyết. Bạn cần phân tích đề bài, xây dựng hàm số mô tả bài toán, và sử dụng đạo hàm để tìm ra nghiệm.
| Hàm số y | Đạo hàm y' |
|---|---|
| C (hằng số) | 0 |
| xn | nxn-1 |
| sin x | cos x |
| cos x | -sin x |
| tan x | 1/cos2x |
| cot x | -1/sin2x |
Giaitoan.edu.vn hy vọng với hướng dẫn chi tiết này, các bạn học sinh sẽ tự tin hơn trong việc giải các bài tập mục 3 trang 42, 43, 44, 45 SGK Toán 11 tập 2. Chúc các bạn học tập tốt!