Chào mừng bạn đến với bài học về Lý thuyết Hai đường thẳng vuông góc trong chương trình SGK Toán 11 tại giaitoan.edu.vn. Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng và quan trọng nhất về mối quan hệ vuông góc giữa hai đường thẳng trong không gian.
Chúng ta sẽ cùng nhau khám phá định nghĩa, điều kiện, tính chất và các ứng dụng thực tế của hai đường thẳng vuông góc. Mục tiêu là giúp bạn hiểu rõ bản chất của vấn đề và có thể áp dụng linh hoạt vào giải các bài tập.
A. Lý thuyết 1. Góc giữa hai đường thẳng
A. Lý thuyết
1. Góc giữa hai đường thẳng
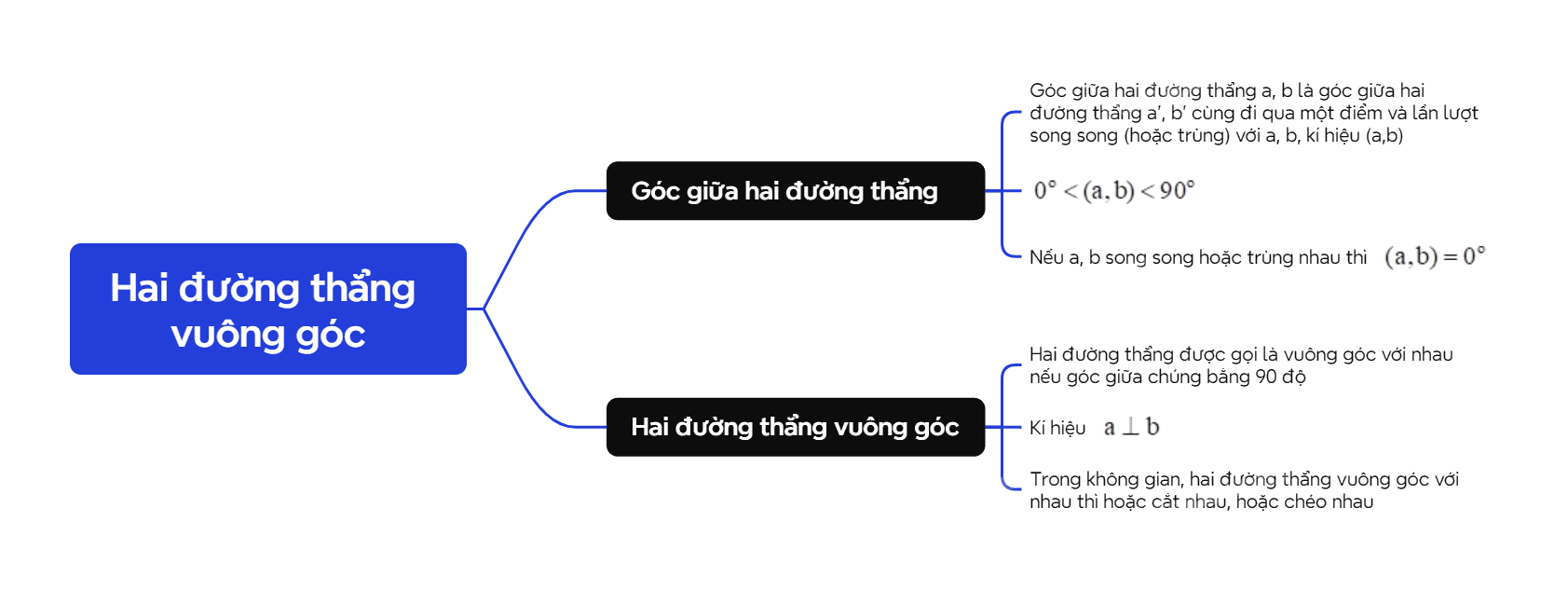
| Góc giữa hai đường thẳng a, b là góc giữa hai đường thẳng a’, b’ cùng đi qua một điểm và lần lượt song song (hoặc trùng) với a, b, kí hiệu (a,b). |
Nhận xét:
+ \({0^o} < (a,b) < {90^o}\).
+ Nếu a, b song song hoặc trùng nhau thì \((a,b) = {0^o}\).
2. Hai đường thẳng vuông góc
| Hai đường thẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng \({90^o}\). |
Lưu ý:
- Khi hai đường thẳng a, b vuông góc với nhau thì ta kí hiệu \(a \bot b\).
- Trong không gian, hai đường thẳng vuông góc với nhau thì hoặc cắt nhau, hoặc chéo nhau.
B. Bài tập
Bài 1: Cho hình hộp ABCD.A’B’C’D’ có ABCD là hình vuông. Tính góc giữa các cặp đường thẳng sau:
a) A’B’ và BC.
b) A’D’ và BD.
c) B’C’ và AD.
Giải:
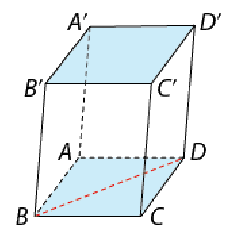
a) Ta có A’B’ // AB, suy ra (A’B’, BC) = (AB, BC).
Mà ABCD là hình vuông nên \(\widehat {ABC} = {90^o}\). Vậy \((A'B',BC) = {90^o}\).
b) Ta có A’D’ // AD, suy ra (A’D’, BD) = (AB, BD).
Mà ABCD là hình vuông nên \(\widehat {ADB} = {45^o}\). Vậy \((A'D',BD) = {45^o}\).
c) Ta có B’C’ // BC và BC // AD nên B’C’ // AD. Vậy \((B'C',AD) = {0^o}\).
Bài 2: Cho tứ diện đều ABCD có cạnh bằng a. Gọi E, F, M, K lần lượt là trung điểm của AB, CD, AC và AD. Chứng minh rằng \(EF \bot MK\).
Giải:
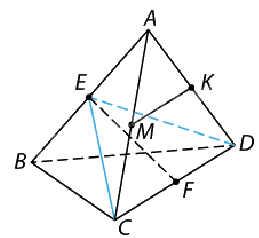
Ta có M và K lần lượt là trung điểm của AC và AD, do đó MK // CD.
Suy ra, góc giữa EF và MN bằng góc giữa EF và CD.
Do ABCD là tứ diện đều cạnh a nên các tam giác ABC và ABD là các tam giác đều cạnh a.
CE và DE là đường trung tuyến đồng thời là đường cao của các tam giác đều cạnh a. Ta tính được \(CE = DE = \frac{{\sqrt 3 }}{2}a\). Vậy tam giác CED cân tại E.
Do F là trung điểm cạnh đáy CD của tam giác cân CED nên \(EF \bot CD\).
Suy ra \((EF,MK) = (EF,CD) = {90^o}\).
Vậy \(EF \bot MK\).
Trong chương trình Toán 11, phần hình học không gian đóng vai trò quan trọng trong việc phát triển tư duy không gian và khả năng giải quyết vấn đề. Một trong những khái niệm cơ bản và then chốt là hai đường thẳng vuông góc. Bài viết này sẽ trình bày chi tiết lý thuyết về hai đường thẳng vuông góc, dựa trên nội dung SGK Toán 11, đồng thời cung cấp các ví dụ minh họa và bài tập để bạn có thể hiểu rõ hơn về chủ đề này.
Hai đường thẳng được gọi là vuông góc với nhau khi và chỉ khi góc giữa chúng bằng 90 độ. Trong không gian, để xác định góc giữa hai đường thẳng, ta thường sử dụng hình chiếu của một đường thẳng lên mặt phẳng chứa đường thẳng kia.
Có nhiều cách để xác định hai đường thẳng vuông góc. Dưới đây là một số điều kiện quan trọng:
Hai đường thẳng vuông góc có những tính chất quan trọng sau:
Lý thuyết về hai đường thẳng vuông góc có nhiều ứng dụng trong thực tế và trong các lĩnh vực khác của toán học:
Bài tập 1: Cho hai đường thẳng d và d' có vector chỉ phương lần lượt là u = (1, 2, -1) và v = (-2, -4, 2). Hai đường thẳng này có vuông góc với nhau không? Tại sao?
Giải: Ta tính tích vô hướng của u và v: u.v = (1)*(-2) + (2)*(-4) + (-1)*(2) = -2 - 8 - 2 = -12. Vì tích vô hướng khác 0, nên hai đường thẳng d và d' không vuông góc với nhau.
Bài tập 2: Cho đường thẳng d vuông góc với mặt phẳng (P). Điểm A nằm trên d. Gọi B là một điểm bất kỳ trên (P). Chứng minh rằng AB vuông góc với mọi đường thẳng nằm trong (P) và đi qua B.
Giải: Vì d vuông góc với (P) tại A, nên d vuông góc với mọi đường thẳng nằm trong (P) và đi qua A. Do đó, d vuông góc với AB. Vì AB nằm trong (P), nên AB vuông góc với mọi đường thẳng nằm trong (P) và đi qua B.
Lý thuyết về hai đường thẳng vuông góc là một phần quan trọng của chương trình Toán 11. Việc nắm vững các định nghĩa, điều kiện, tính chất và ứng dụng của khái niệm này sẽ giúp bạn giải quyết các bài toán hình học không gian một cách hiệu quả và chính xác. Hãy luyện tập thường xuyên và áp dụng kiến thức vào thực tế để hiểu sâu hơn về chủ đề này. Chúc bạn học tốt tại giaitoan.edu.vn!