Bài 4.9 trang 100 SGK Toán 11 tập 1 là một bài tập quan trọng trong chương trình học Toán 11, tập trung vào việc vận dụng kiến thức về đường thẳng và mặt phẳng trong không gian. Bài tập này đòi hỏi học sinh phải nắm vững các khái niệm, định lý và phương pháp giải liên quan.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu và phương pháp giải nhanh chóng cho Bài 4.9 trang 100 SGK Toán 11 tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi M là một điểm di động trên cạnh SC.
Đề bài
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi M là một điểm di động trên cạnh SC.
a) Tìm giao điểm N của SD và mặt phẳng (ABM).
b) Gọi I là giao điểm của hai đường thẳng BM và AN. Chứng minh rằng I nằm trên một đường thẳng cố định khi M di động trên cạnh SC.
Phương pháp giải - Xem chi tiết
Cách tìm giao điểm của một đường thẳng a với một mặt phẳng (P):
+ Bước 1: Tìm \(\left( Q \right) \supset a\). Tìm \(d = \left( P \right) \cap \left( Q \right)\)
+ Bước 2: Tìm \(I = a \cap d\). I chính là giao điểm của a và (P).
Lời giải chi tiết
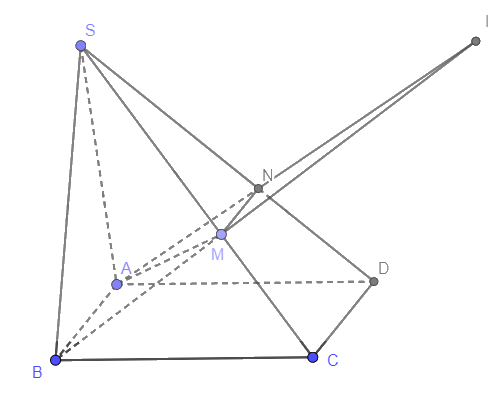
a) Ta có:
\(\left\{ \begin{array}{l}M \in \left( {SCD} \right) \cap \left( {ABM} \right)\\AB \subset \left( {ABM} \right)\\CD \subset \left( {SCD} \right)\\AB//CD\end{array} \right.\)
Suy ra giao tuyến của (SCD) và (ABM) là đường thẳng d đi qua M là song song với AB, BC.
Vậy N là giao điểm của đường thẳng d và SD.
b) (SAD) và (SBC) có chung điểm S và AD//BC. Nên giao tuyến của (SAD) và (SBC) là đường thẳng đi qua S và song song với AD, BC.
Ta có: \(\left\{ \begin{array}{l}I = BM \cap AN\\BM \subset \left( {SBC} \right)\\AN \subset \left( {SAD} \right)\end{array} \right.\)
Suy ra I nằm trên giao tuyến của (SBC) và (SAD) chính là đường thẳng đi qua S và song song với AD, BC.
Vì S, AD cố định nên I luôn nằm trên đường thẳng cố định đi qua S và song song với AD.
Bài 4.9 trang 100 SGK Toán 11 tập 1 yêu cầu giải quyết một bài toán liên quan đến việc xác định mối quan hệ giữa đường thẳng và mặt phẳng trong không gian. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản sau:
Phân tích bài toán:
Trước khi bắt tay vào giải bài toán, chúng ta cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Sau đó, chúng ta cần phân tích bài toán để tìm ra hướng giải phù hợp. Thông thường, chúng ta có thể sử dụng các phương pháp sau:
Lời giải chi tiết:
(Nội dung lời giải chi tiết bài 4.9 trang 100 SGK Toán 11 tập 1 sẽ được trình bày tại đây, bao gồm các bước giải, giải thích rõ ràng và minh họa bằng hình vẽ nếu cần thiết. Lời giải sẽ được trình bày một cách logic và dễ hiểu, giúp học sinh nắm vững kiến thức và phương pháp giải.)
Ví dụ minh họa:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài toán, chúng ta sẽ xem xét một ví dụ minh họa:
(Ví dụ minh họa sẽ được trình bày tại đây, bao gồm đề bài, lời giải chi tiết và giải thích rõ ràng.)
Bài tập tương tự:
Để rèn luyện kỹ năng giải bài toán, các em học sinh có thể tự giải các bài tập tương tự sau:
Kết luận:
Bài 4.9 trang 100 SGK Toán 11 tập 1 là một bài tập quan trọng trong chương trình học Toán 11. Việc nắm vững kiến thức và phương pháp giải bài toán này sẽ giúp các em học sinh tự tin giải các bài tập tương tự và đạt kết quả tốt trong các kỳ thi.
Hy vọng rằng, với lời giải chi tiết và phân tích kỹ lưỡng mà giaitoan.edu.vn cung cấp, các em học sinh sẽ hiểu rõ hơn về Bài 4.9 trang 100 SGK Toán 11 tập 1 và có thể tự tin giải các bài tập tương tự.
Để hiểu rõ hơn về bài toán này, bạn cần nắm vững các khái niệm sau:
Khi giải các bài tập về đường thẳng và mặt phẳng, bạn cần lưu ý những điều sau: