Chào mừng các em học sinh đến với bài giải chi tiết mục 3 trang 68, 69 SGK Toán 11 tập 2 tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải đầy đủ, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Bài học này tập trung vào các kiến thức quan trọng của chương trình Toán 11, đặc biệt là các ứng dụng của đạo hàm trong việc khảo sát hàm số. Hãy cùng chúng tôi khám phá và chinh phục những bài toán thú vị này nhé!
Quan sát Hình 8.41.
Quan sát Hình 8.41.
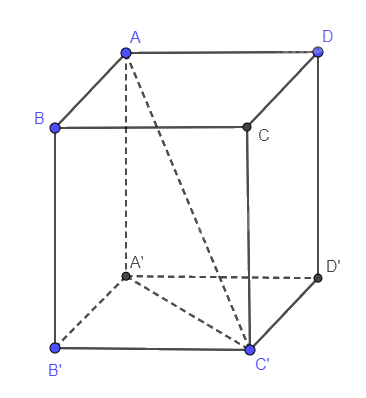
Xét hình lăng trụ (3). Biết rằng lăng trụ này có hai mặt bên chung cạnh AA’ là hai hình chữ nhật.
a) Cạnh AA' có vuông góc với mặt đáy không? Vì sao?
b) Các mặt bên còn lại là những hình gì? Vì sao?
Phương pháp giải:
a) Nếu một đường thẳng vuông góc với 2 đường thẳng cắt nhau cùng nằm trong một mặt phẳng thì nó vuông góc với mặt phẳng ấy.
b) Hình lăng trụ có các cạnh bên song song với nhau và các mặt bên là hình bình hành.
Lời giải chi tiết:
a) Vì AA’ vuông góc với AB và AE nên AA’ vuông góc với (ABCDE).
b) Hình lăng trụ có các cạnh bên song song với nhau và các mặt bên là hình bình hành. Mà AA’ vuông góc với đáy nên các cạnh bên còn lại cũng vuông góc với đáy. Suy ra các mặt bên là hình chữ nhật.
Tính độ dài đường chéo của hình hộp chữ nhật ABCD.A’B’C’D’ biết AA’ = 6a, AD = 3a, AB = 2a.
Phương pháp giải:
Áp dụng định lý Py-ta-go để tính A’C’. Từ đó tính AC.
Lời giải chi tiết:

ABCD.A’B’C’D’ là hình hộp chữ nhật nên A’B’ = AB = 2a, B’C’ = BC = 3a
Xét tam giác A’B’C’ vuông tại B’ có:
\(A'C = \sqrt {A'B{'^2} + B'C{'^2}} = \sqrt {{{\left( {2a} \right)}^2} + {{\left( {3a} \right)}^2}} = \sqrt {13} a\)
Xét tam giác AA’C vuông tại A’ có:
\(AC = \sqrt {AA{'^2} + A'{C^2}} = \sqrt {{{\left( {6a} \right)}^2} + {{\left( {\sqrt {13} a} \right)}^2}} = 7a\)
Mục 3 trang 68, 69 SGK Toán 11 tập 2 tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế liên quan đến khảo sát hàm số. Cụ thể, các bài tập trong mục này thường yêu cầu học sinh xác định khoảng đồng biến, nghịch biến, cực trị của hàm số, từ đó vẽ được đồ thị hàm số một cách chính xác.
Để hiểu rõ hơn về nội dung và phương pháp giải các bài tập trong mục 3, chúng ta sẽ đi vào phân tích chi tiết từng bài tập:
Bài tập này yêu cầu học sinh khảo sát hàm số bậc ba, bao gồm các bước sau:
Trong quá trình giải bài tập này, học sinh cần nắm vững các kiến thức về đạo hàm, điểm cực trị và bảng biến thiên.
Bài tập này yêu cầu học sinh khảo sát hàm số hữu tỉ, với các bước tương tự như bài tập 1. Tuy nhiên, cần lưu ý thêm một số điểm sau:
Việc xác định tiệm cận và nghiên cứu giới hạn là rất quan trọng để vẽ được đồ thị hàm số hữu tỉ một cách chính xác.
Bài tập này yêu cầu học sinh sử dụng kiến thức về khảo sát hàm số để giải phương trình. Phương pháp giải thường được sử dụng là vẽ đồ thị hàm số và tìm giao điểm của đồ thị với trục hoành.
Để giải các bài tập khảo sát hàm số một cách hiệu quả, học sinh cần:
Xét hàm số y = x3 - 3x2 + 2. Để khảo sát hàm số này, ta thực hiện các bước sau:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + | |
| y | ↗ | ↘ | ↗ |
Từ bảng biến thiên, ta thấy hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2). Hàm số đạt cực đại tại x = 0 và cực tiểu tại x = 2.
Việc giải các bài tập trong mục 3 trang 68, 69 SGK Toán 11 tập 2 đòi hỏi học sinh phải nắm vững các kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em sẽ tự tin hơn trong việc giải quyết các bài toán này. Chúc các em học tập tốt!