Bài 8.41 trang 89 SGK Toán 11 tập 2 là một bài tập quan trọng trong chương trình học Toán 11, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, cùng với các phương pháp giải nhanh chóng và hiệu quả, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
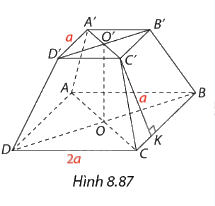
Cho hình chóp cụt đều (Hình 8.87) có hai đáy là các hình vuông cạnh 2a và a. Chiều cao của mặt bên bằng a. Tính:
Đề bài
Cho hình chóp cụt đều (Hình 8.87) có hai đáy là các hình vuông cạnh 2a và a. Chiều cao của mặt bên bằng a. Tính:
a) Thể tích của khối chóp cụt đều này;
b) Số đo của các góc nhị diện tạo bởi mặt bên và các mặt đáy của hình chóp cụt đều này.
Phương pháp giải - Xem chi tiết
Công thức tính thể tích hình chóp cụt: \(V = \frac{1}{3}h\left( {S + S' + \sqrt {SS'} } \right)\) với h là chiều cao, S là diện tích đáy nhỏ, S’ là diện tích đáy lớn.
Lời giải chi tiết
a) \(V = \frac{1}{3}h\left( {S + S' + \sqrt {SS'} } \right) = \frac{1}{3}.a.\left( {{a^2} + 4{a^2}} \right) = \frac{5}{3}{a^3}\)
b) OK vuông góc với BC, C’K vuông góc với BC nên góc phẳng nhị diện cần tìm là góc OKC’
Bài 8.41 trang 89 SGK Toán 11 tập 2 yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để tìm cực trị và khảo sát hàm số. Bài toán này thường xuất hiện trong các đề thi và kiểm tra, do đó việc nắm vững phương pháp giải là vô cùng quan trọng.
Trước khi bắt đầu giải bài toán, chúng ta cần phân tích kỹ đề bài để xác định rõ yêu cầu và các thông tin đã cho. Trong bài 8.41, đề bài thường yêu cầu tìm cực trị của hàm số, xác định khoảng đồng biến, nghịch biến và vẽ đồ thị hàm số.
Bước 1: Tính đạo hàm cấp một
y' = 3x^2 - 6x
Bước 2: Tìm điểm dừng
3x^2 - 6x = 0
3x(x - 2) = 0
=> x = 0 hoặc x = 2
Bước 3: Khảo sát dấu của y'
Xét khoảng (-∞; 0): y' > 0 => Hàm số đồng biến
Xét khoảng (0; 2): y' < 0 => Hàm số nghịch biến
Xét khoảng (2; +∞): y' > 0 => Hàm số đồng biến
Bước 4: Tìm cực trị
Tại x = 0, y' đổi dấu từ dương sang âm => x = 0 là điểm cực đại, y(0) = 2
Tại x = 2, y' đổi dấu từ âm sang dương => x = 2 là điểm cực tiểu, y(2) = -2
Bước 5: Tính đạo hàm cấp hai
y'' = 6x - 6
Bước 6: Khảo sát tính lồi, lõm
Xét khoảng (-∞; 1): y'' < 0 => Hàm số lõm
Xét khoảng (1; +∞): y'' > 0 => Hàm số lồi
Bước 7: Vẽ đồ thị hàm số
Dựa vào các thông tin trên, ta có thể vẽ được đồ thị hàm số y = x^3 - 3x^2 + 2.
Đạo hàm có rất nhiều ứng dụng trong thực tế, như:
Việc nắm vững kiến thức về đạo hàm không chỉ giúp bạn giải quyết các bài tập Toán học mà còn mở ra nhiều cơ hội ứng dụng trong các lĩnh vực khác.
Hy vọng với lời giải chi tiết và phương pháp giải rõ ràng này, bạn sẽ tự tin hơn khi giải Bài 8.41 trang 89 SGK Toán 11 tập 2 và các bài tập tương tự. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình.