Chào mừng bạn đến với bài học về Lý thuyết Các phép biến đổi lượng giác trong chương trình SGK Toán 11. Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng và quan trọng nhất về các phép biến đổi lượng giác, giúp bạn giải quyết các bài toán liên quan một cách hiệu quả.
Chúng tôi tại giaitoan.edu.vn cam kết mang đến cho bạn những bài giảng chất lượng, dễ hiểu và được trình bày một cách logic, giúp bạn tiếp thu kiến thức một cách nhanh chóng và hiệu quả.
1. Công thức cộng
1. Công thức cộng
\(\begin{array}{l}\sin \left( {a + b} \right) = \sin a\cos b + \cos asinb\\sin\left( {a - b} \right) = \sin a\cos b - \cos asinb\\\cos \left( {a + b} \right) = \cos a\cos b - \sin asinb\\\cos \left( {a - b} \right) = \cos a\cos b + \sin asinb\\\tan \left( {a + b} \right) = \frac{{\tan a + \tan b}}{{1 - \tan a\tan b}}\\\tan \left( {a - b} \right) = \frac{{\tan a - \tan b}}{{1 + \tan a\tan b}}\end{array}\)
2. Công thức nhân đôi
\(\begin{array}{l}\sin 2a = 2\sin a\cos a\\\cos 2a = {\cos ^2}a - {\sin ^2}a = 2{\cos ^2}a - 1 = 1 - 2{\sin ^2}a\\\tan 2a = \frac{{2\tan a}}{{1 - {{\tan }^2}a}}\end{array}\)
Suy ra, công thức hạ bậc:
\({\sin ^2}a = \frac{{1 - \cos 2a}}{2},{\cos ^2}a = \frac{{1 + \cos 2a}}{2}\)
3. Công thức biến đổi tích thành tổng
\(\begin{array}{l}\cos a\cos b = \frac{1}{2}\left[ {\cos \left( {a + b} \right) + \cos \left( {a - b} \right)} \right]\\\sin a\sin b = \frac{1}{2}\left[ {\cos \left( {a - b} \right) - \cos \left( {a + b} \right)} \right]\\\sin a\cos b = \frac{1}{2}\left[ {\sin \left( {a + b} \right) + \sin \left( {a - b} \right)} \right]\end{array}\)
4. Công thức biến đổi tổng thành tích
\(\begin{array}{l}\cos a + \cos b = 2\cos \frac{{a + b}}{2}\cos \frac{{a - b}}{2}\\\cos a - \cos b = - 2\sin \frac{{a + b}}{2}\sin \frac{{a - b}}{2}\\\sin a + \sin b = 2\sin \frac{{a + b}}{2}\cos \frac{{a - b}}{2}\\\sin a - \sin b = 2\cos \frac{{a + b}}{2}\sin \frac{{a - b}}{2}\end{array}\)
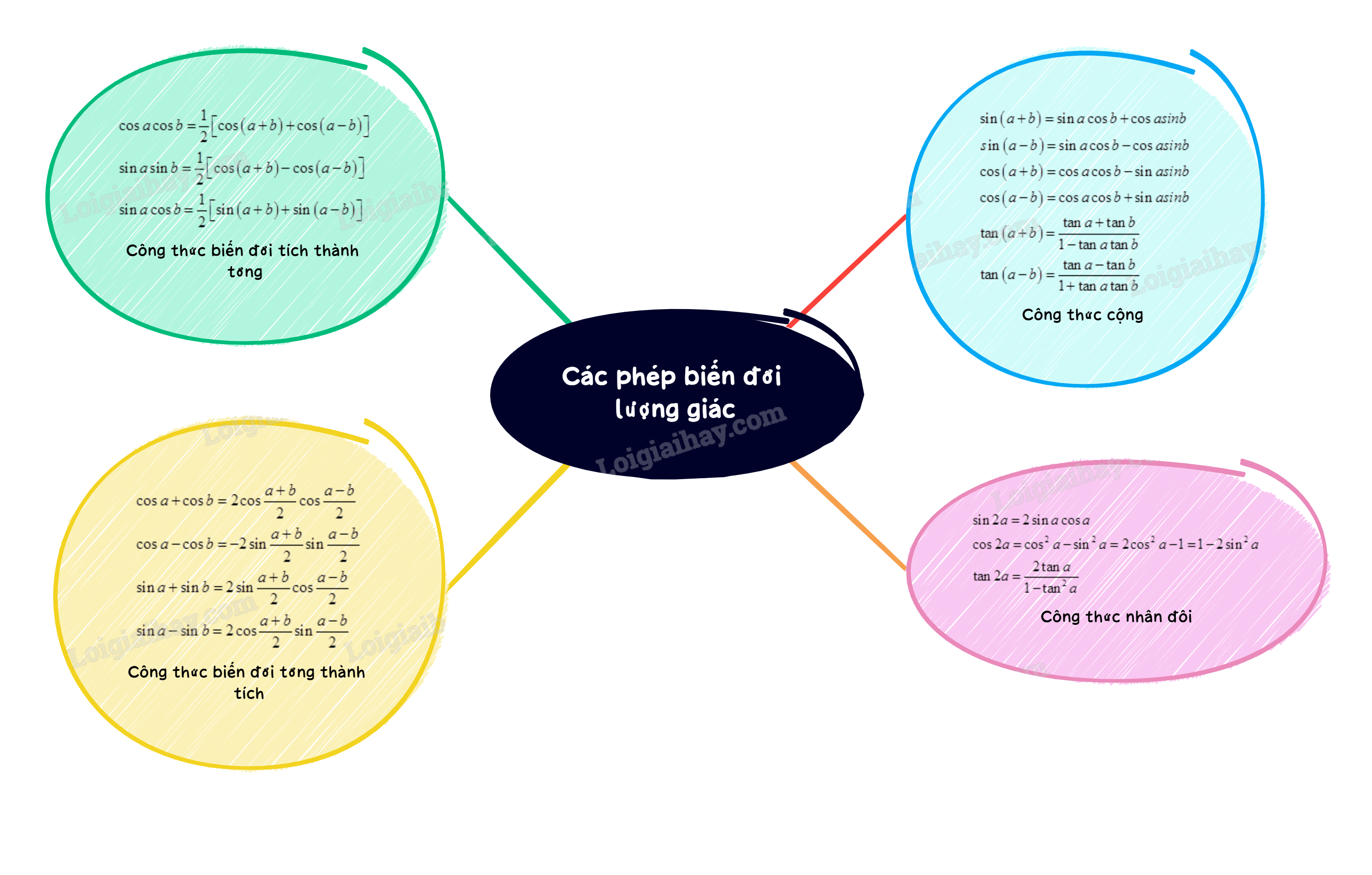
Các phép biến đổi lượng giác đóng vai trò quan trọng trong chương trình Toán 11, là nền tảng cho việc giải quyết nhiều bài toán phức tạp hơn trong các chương trình học nâng cao. Bài viết này sẽ trình bày chi tiết lý thuyết về các phép biến đổi lượng giác, bao gồm công thức cộng, trừ, nhân đôi, chia đôi, và các công thức liên quan khác.
Trước khi đi vào các phép biến đổi lượng giác, chúng ta cần nắm vững các công thức lượng giác cơ bản sau:
Các công thức cộng và trừ lượng giác cho phép chúng ta tính giá trị của các hàm lượng giác của tổng hoặc hiệu của hai góc:
Công thức nhân đôi lượng giác cho phép chúng ta tính giá trị của các hàm lượng giác của hai lần một góc:
Công thức chia đôi lượng giác cho phép chúng ta tính giá trị của các hàm lượng giác của một nửa góc:
Ngoài các công thức trên, còn có một số công thức biến đổi lượng giác khác thường được sử dụng:
Các phép biến đổi lượng giác có nhiều ứng dụng trong toán học và các lĩnh vực khác, bao gồm:
Để hiểu rõ hơn về các phép biến đổi lượng giác, chúng ta hãy xem xét một số bài tập ví dụ:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cần thiết về Lý thuyết Các phép biến đổi lượng giác - SGK Toán 11. Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng vào giải quyết các bài toán thực tế.