Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 của giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau khám phá và giải chi tiết các bài tập trong mục 1 trang 24 và 25 của sách giáo khoa Toán 11 tập 2.
Mục tiêu của chúng tôi là giúp các em hiểu rõ kiến thức, nắm vững phương pháp giải bài tập và tự tin hơn trong quá trình học tập môn Toán.
Quan sát các đồ thị ở trên và hãy biện luận theo b số giao điểm của đồ thị hàm số \(y = {\log _a}x\) và đường thẳng y = b.
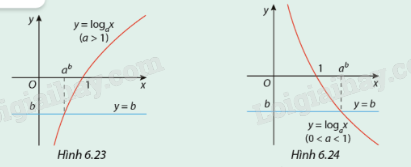
Quan sát các đồ thị ở trên và hãy biện luận theo b số giao điểm của đồ thị hàm số \(y = {\log _a}x\) và đường thẳng y = b.
Phương pháp giải:
Quan sát hình vẽ.
Lời giải chi tiết:
Xét phương trình hoành độ giao điểm \({\log _a}x = b\)
Phương trình luôn có nghiệm duy nhất \(x = {a^b}\forall b\)
Giải các phương trình
a) \({\log _2}\left( {2x + 6} \right) + {\log _2}x = 3\)
b) \(\log x = \log \left( {{x^2} + x - 1} \right)\)
Phương pháp giải:
\(b = {\log _a}A \Leftrightarrow {\log _a}A = {\log _a}B \Leftrightarrow \left\{ \begin{array}{l}A > 0\\B > 0\\A = B\end{array} \right.\)
Lời giải chi tiết:
a) Điều kiện: \(\left\{ \begin{array}{l}2x + 6 > 0\\x > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > - 3\\x > 0\end{array} \right. \Leftrightarrow x > 0\)
\(\begin{array}{l}{\log _2}\left( {2x + 6} \right) + {\log _2}x = 3\\ \Leftrightarrow {\log _2}\left[ {\left( {2x + 6} \right)x} \right] = {\log _2}8\\ \Leftrightarrow 2{x^2} + 6x = 8\\ \Leftrightarrow 2{x^2} + 6x - 8 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\left( {{\rm{TM}}} \right)\\x = - 4\left( {\rm{L}} \right)\end{array} \right.\end{array}\)
Vậy phương trình có nghiệm là x = 1
b) Điều kiện: x > 0
\(\begin{array}{l}\log x = \log \left( {{x^2} + x - 1} \right)\\ \Leftrightarrow x = {x^2} + x - 1\\ \Leftrightarrow {x^2} - 1 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\left( {{\rm{TM}}} \right)\\x = - 1\left( {\rm{L}} \right)\end{array} \right.\end{array}\)
Vậy phương trình có tập nghiệm là x = 1
Mục 1 của SGK Toán 11 tập 2 thường tập trung vào một chủ đề quan trọng trong chương trình học. Để giải quyết các bài tập trong mục này một cách hiệu quả, trước hết chúng ta cần nắm vững lý thuyết cơ bản và các định nghĩa liên quan. Việc hiểu rõ bản chất của vấn đề sẽ giúp chúng ta lựa chọn phương pháp giải phù hợp.
Các bài tập trong mục 1 thường yêu cầu học sinh vận dụng kiến thức lý thuyết để giải quyết các bài toán cụ thể. Một số phương pháp giải bài tập thường gặp bao gồm:
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 1 trang 24 và 25 SGK Toán 11 tập 2. Chúng tôi sẽ trình bày lời giải một cách rõ ràng, dễ hiểu, kèm theo các bước giải cụ thể và giải thích chi tiết.
Đề bài: ...
Lời giải: ...
Đề bài: ...
Lời giải: ...
Đề bài: ...
Lời giải: ...
Đề bài: ...
Lời giải: ...
Sau khi đã xem lời giải chi tiết của các bài tập trong mục 1, các em nên tự mình luyện tập thêm để củng cố kiến thức và rèn luyện kỹ năng giải bài tập. Các em có thể tìm thêm các bài tập tương tự trong sách bài tập hoặc trên các trang web học toán online.
Hy vọng rằng với bài viết này, các em đã nắm vững kiến thức và kỹ năng giải bài tập trong mục 1 trang 24, 25 SGK Toán 11 tập 2. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục tri thức. Hãy truy cập website của chúng tôi để khám phá thêm nhiều tài liệu học tập hữu ích khác.