Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 1 của giaitoan.edu.vn. Ở đây, chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho tất cả các bài tập trong SGK, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Mục 2 của chương trình Toán 11 tập 1 thường xoay quanh các chủ đề quan trọng như phép biến hình, hàm số bậc hai và ứng dụng của chúng. Việc giải đúng các bài tập trong mục này là nền tảng vững chắc cho các kiến thức nâng cao hơn.
Cho hai đường thẳng \(d\) và \(d'\) song song với nhau và một mặt phẳng \(\left( \alpha \right)\) chứa \(d'\)nhưng không chứa \(d\). Gọi \(\left( \beta \right)\) là mặt phẳng chứa \(d\) và \(d'\).
Cho hai đường thẳng \(d\) và \(d'\) song song với nhau và một mặt phẳng \(\left( \alpha \right)\) chứa \(d'\)nhưng không chứa \(d\). Gọi \(\left( \beta \right)\) là mặt phẳng chứa \(d\) và \(d'\).
a) Xác định giao tuyến của \(\left( \alpha \right)\) và \(\left( \beta \right)\).
b) \(d\) và \(\left( \alpha \right)\) có điểm chung hay không? Vì sao ?
Phương pháp giải:
a) Đường thẳng cùng thuộc 2 mặt phẳng là giao tuyến của 2 mặt phẳng đó.
b) Chứng minh phản chứng (Giả sử không có điểm chung).
Lời giải chi tiết:
a) \(\left\{ \begin{array}{l}d' \subset \left( \alpha \right)\\d' \subset \left( \beta \right)\end{array} \right. \Rightarrow d' = \left( \alpha \right) \cap \left( \beta \right)\)
Vậy \(d'\) là giao tuyến của \(\left( \alpha \right)\) và \(\left( \beta \right)\).
b) Giả sử \(d\) và \(\left( \alpha \right)\) có diểm chung là I
Mà \(I \in d \subset \left( \beta \right)\) \( \Rightarrow \)I là điểm chung của \(\left( \alpha \right)\) và \(\left( \beta \right)\)\( \Rightarrow \)I phải thuộc \(d'\)
\( \Rightarrow \)\(d\) và \(d'\) có điểm chung là I (Mâu thuẫn)
Vậy \(d\) và \(\left( \alpha \right)\) không có diểm chung.
Cho tứ diện ABCD. Gọi M, N, P lần lượt là trung điểm của AB, AC, AD. Các đường thẳng MN, NP, PM có song song với mặt phẳng (BCD) không? Vì sao?
Phương pháp giải:
Nếu đường thẳng a không nằm trong (P) và a song song với đường thẳng b nằm trong (P) thì a song song với (P).
Lời giải chi tiết:
Xét tam giác ABC có M, N lần lượt là trung điểm của AB, AC \( \Rightarrow \)MN // BC
Mà BC nằm trong (BCD) nên MN // (BCD).
Xét tam giác ABD có M, P lần lượt là trung điểm của AB, AD \( \Rightarrow \)MP // BD
Mà BD nằm trong (BCD) nên MP // (BCD).
Xét tam giác ADC có P, N lần lượt là trung điểm của AD, AC \( \Rightarrow \)PN // CD
Mà CD nằm trong (BCD) nên PN // (BCD).
Cho đường thẳng a song song với mặt phẳng \(\left( \alpha \right)\). Gọi \(\left( \beta \right)\) là mặt phẳng chứa a và \(\left( \beta \right)\) cắt \(\left( \alpha \right)\) theo giao tuyến b. Hỏi b và a có thể có điểm chung hay không? Vì sao?
Phương pháp giải:
Chứng minh phản chứng (Giả sử có điểm chung).
Lời giải chi tiết:
Giả sử a và b có điểm chung là I
b là giao tuyến của \(\left( \beta \right)\) cắt \(\left( \alpha \right)\) nên I cũng phải thuộc \(\left( \alpha \right)\)
Suy ra a và \(\left( \alpha \right)\) có điểm chung là I (Mâu thuẫn)
Vậy a không có điểm chung với b.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Lấy I là điểm thuộc cạnh BC (khác B và C). Gọi \(\left( \alpha \right)\) là mặt phẳng qua I và song song với các đường thẳng AB và SD. Tìm giao điểm của các đường thẳng AD, SA, SB với mặt phẳng \(\left( \alpha \right)\).
Phương pháp giải:
Xác định giao điểm của một mặt phẳng (P) song song với a, đi qua O và đường thẳng b:
+ Tìm một mặt phẳng (Q) chứa O (hoặc một điểm thuộc (P)), a, b.
+ Giao tuyến của (P) và (Q) là đường thẳng d đi qua O (hoặc một điểm thuộc (P)) và song song với a.
+ Tìm giao điểm của b và d. Đây chính là giao điểm cần tìm.
Lời giải chi tiết:

\(\left( \alpha \right)\) đi qua I và song song với AB nên \(\left( \alpha \right)\) cắt (ABCD) theo giao tuyến d đi qua I và song song với AB. Gọi E là giao điểm của d với AB. Vậy E là giao điểm của AD và \(\left( \alpha \right)\).
\(\left( \alpha \right)\) song song với SD nên \(\left( \alpha \right)\) cắt (SAD) theo giao tuyến d’ đi qua E và song song với SD. Gọi F là giao điểm của d’ với SA. Vậy F là giao điểm của SA và \(\left( \alpha \right)\).
\(\left( \alpha \right)\) song song với AB nên \(\left( \alpha \right)\) cắt (SAB) theo giao tuyến d’’ đi qua F và song song với AB. Gọi G là giao điểm của d’’ với SB. Vậy G là giao điểm của SB và \(\left( \alpha \right)\).
Cho hai đường thẳng chéo nhau a và b. Lấy điểm M bất kì thuộc a. Qua M kẻ đường thẳng b′ song song với b. Gọi \(\left( \alpha \right)\) là mặt phẳng xác định bởi a và b′. Hãy nhận xét về vị trí tương đối của b và \(\left( \alpha \right)\)?

Phương pháp giải:
Nếu đường thẳng a không nằm trong (P) và a song song với đường thẳng b nằm trong (P) thì a song song với (P).
Lời giải chi tiết:
\(\left\{ \begin{array}{l}b' \subset \left( \alpha \right)\\b \not\subset \left( \alpha \right)\\b//b'\end{array} \right. \Rightarrow b//\left( \alpha \right)\)
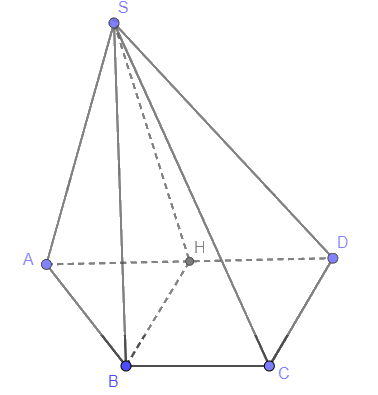
Cho hình chóp S.ABCD có đáy là hình thang ABCD, AD song song BC và AD = 2BC. Xác định mặt phẳng chứa SB và song song với CD.
Phương pháp giải:
Dựng một mặt phẳng chứa SB và chứa 1 đường thẳng song song với CD.
Lời giải chi tiết:

Gọi H là trung điểm AD, ta có HD // BC và HD = \(\frac{1}{2}\)AD = BC nên HDCB là hình bình hành.
Suy ra HB // CD, mà (SBH) chứa SB nên CD // (SBH).
Vậy (SBH) là mặt phẳng chứa SB và song song với CD.
Trong giờ ra chơi, khi thảo luận về hình học không gian, bạn An khẳng định rằng : “Hai đường thẳng phân biệt cùng song song với một mặt phẳng thì chúng song song với nhau”. Bạn Mai cho rằng đây là một khẳng định sai, Mai muốn tìm các hình ảnh về đường thẳng và mặt phẳng trong thực tế để minh hoạ cho ý kiến của mình. Dựa vào các đồ vật xung quanh phòng học, hãy giúp Mai chỉ ra một ví dụ để thấy khẳng định của An là sai.
Phương pháp giải:
Quan sát thực tế.
Lời giải chi tiết:
Mép tường trái/phải và mép tường trên/dưới của một bức tường luôn song song với một mặt phẳng là bức tường đối diện nhưng chúng không song song với nhau.
Mục 2 trong SGK Toán 11 tập 1 là một phần quan trọng, tập trung vào việc củng cố kiến thức về hàm số bậc hai, các phép biến hình và ứng dụng của chúng trong giải quyết các bài toán thực tế. Việc nắm vững các khái niệm và kỹ năng trong mục này là nền tảng cho việc học tập các kiến thức toán học nâng cao hơn ở các lớp trên.
Mục 2 thường bao gồm các nội dung sau:
Dưới đây là phần giải chi tiết các bài tập trong Mục 2, trang 102, 103, 104, 105 SGK Toán 11 tập 1:
(Nội dung bài tập và lời giải chi tiết)
(Nội dung bài tập và lời giải chi tiết)
(Nội dung bài tập và lời giải chi tiết)
(Nội dung bài tập và lời giải chi tiết)
(Nội dung bài tập và lời giải chi tiết)
(Nội dung bài tập và lời giải chi tiết)
(Nội dung bài tập và lời giải chi tiết)
(Nội dung bài tập và lời giải chi tiết)
Để giải các bài tập về hàm số bậc hai một cách hiệu quả, các em cần nắm vững các kiến thức sau:
Các phép biến hình đóng vai trò quan trọng trong việc giải quyết nhiều bài toán hình học. Các em cần nắm vững các tính chất của từng phép biến hình để áp dụng một cách linh hoạt:
Để học tốt môn Toán 11, các em nên:
Hy vọng với những giải thích chi tiết và hướng dẫn cụ thể trên đây, các em sẽ tự tin hơn trong việc giải các bài tập Mục 2 trang 102, 103, 104, 105 SGK Toán 11 tập 1. Chúc các em học tập tốt!