Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 của giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau đi sâu vào việc giải chi tiết các bài tập trong mục 1, trang 21 và 22 của sách giáo khoa Toán 11 tập 2.
Mục tiêu của chúng ta là không chỉ tìm ra đáp án đúng mà còn hiểu rõ phương pháp giải, từ đó áp dụng vào các bài tập tương tự một cách hiệu quả. Hãy cùng bắt đầu!
Quan sát các đồ thị ở trên và hãy biện luận theo b số giao điểm của đồ thị hàm số \(y = {a^x}\) và đường thẳng y = b.
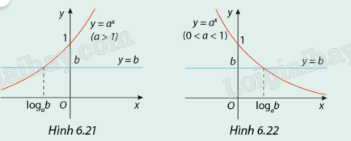
Quan sát các đồ thị ở trên và hãy biện luận theo b số giao điểm của đồ thị hàm số \(y = {a^x}\) và đường thẳng y = b.
Phương pháp giải:
Quan sát hình vẽ.
Lời giải chi tiết:
Ta có phương trình hoành độ giao điểm \({a^x} = b\)
Nếu b > 0 thì phương trình có nghiệm duy nhất là \(x = {\log _a}b\)
Nếu \(b \le 0\)thì phương trình vô nghiệm.
Giải các phương trình:
a) \({2.3^{x + 1}} - {6.3^{x - 1}} - {3^x} = 9\)
b) \(1,{5^{5x - 7}} = {\left( {\frac{2}{3}} \right)^{x + 1}}\)
Phương pháp giải:
Với \(a > 0,a \ne 1\), ta có: \({a^{A\left( x \right)}} = {a^{B\left( x \right)}} \Leftrightarrow A\left( x \right) = B\left( x \right)\,\)
Lời giải chi tiết:
a)
\(\begin{array}{l}{2.3^{x + 1}} - {6.3^{x - 1}} - {3^x} = 9\\ \Leftrightarrow {2.3^2}{.3^{x - 1}} - {6.3^{x - 1}} - {3.3^{x - 1}} = 9\\ \Leftrightarrow {3^{x - 1}}\left( {{{2.3}^2} - 6 - 3} \right) = 9\\ \Leftrightarrow {3^{x - 1}}.9 = 9\\ \Leftrightarrow {3^{x - 1}} = 1\\ \Leftrightarrow {3^{x - 1}} = {3^0}\\ \Leftrightarrow x - 1 = 0\\ \Leftrightarrow x = 1\end{array}\)
Vậy phương trình có nghiệm là x = 1.
b)
\(\begin{array}{l}1,{5^{5x - 7}} = {\left( {\frac{2}{3}} \right)^{x + 1}}\\ \Leftrightarrow {\left( {\frac{1}{{\frac{2}{3}}}} \right)^{5x - 7}} = {\left( {\frac{2}{3}} \right)^{x + 1}}\\ \Leftrightarrow \frac{1}{{{{\left( {\frac{2}{3}} \right)}^{5x - 7}}}} = {\left( {\frac{2}{3}} \right)^{x + 1}}\\ \Leftrightarrow {\left( {\frac{2}{3}} \right)^{x + 1}}.{\left( {\frac{2}{3}} \right)^{5x - 7}} = 1\\ \Leftrightarrow {\left( {\frac{2}{3}} \right)^{6x - 6}} = {\left( {\frac{2}{3}} \right)^0}\\ \Leftrightarrow 6x - 6 = 0\\ \Leftrightarrow x = 1\end{array}\)
Vậy phương trình có nghiệm x = 1.
Mục 1 của SGK Toán 11 tập 2 thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này một cách hiệu quả, học sinh cần nắm vững kiến thức lý thuyết liên quan, bao gồm định nghĩa, tính chất, định lý và các công thức quan trọng. Việc ôn tập lại lý thuyết trước khi bắt tay vào giải bài tập là một bước chuẩn bị cần thiết.
Trang 21 thường chứa các bài tập vận dụng kiến thức cơ bản để kiểm tra mức độ hiểu bài của học sinh. Các bài tập có thể bao gồm:
Ví dụ, một bài tập thường gặp có thể là:
Cho hàm số y = f(x). Tìm đạo hàm của hàm số tại điểm x = a.
Để giải bài tập này, học sinh cần áp dụng định nghĩa đạo hàm hoặc các quy tắc tính đạo hàm đã học.
Trang 22 thường chứa các bài tập nâng cao, đòi hỏi học sinh phải vận dụng kiến thức một cách linh hoạt và sáng tạo. Các bài tập có thể bao gồm:
Ví dụ, một bài tập thường gặp có thể là:
Giải phương trình: sin(2x) = cos(x).
Để giải bài tập này, học sinh cần sử dụng các công thức lượng giác và kỹ năng biến đổi phương trình.
Để giải bài tập Toán 11 tập 2 một cách hiệu quả, học sinh có thể áp dụng các phương pháp sau:
Toán 11 tập 2 là một môn học quan trọng, đòi hỏi sự nỗ lực và kiên trì. Để học tốt môn học này, học sinh nên:
Hy vọng rằng với những hướng dẫn chi tiết và phương pháp giải bài tập hiệu quả trên đây, các em học sinh sẽ tự tin hơn khi đối mặt với các bài tập trong mục 1 trang 21, 22 SGK Toán 11 tập 2. Chúc các em học tập tốt và đạt kết quả cao!