Bài 6.11 trang 19 SGK Toán 11 tập 2 thuộc chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến phép biến hình. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để xác định ảnh của một điểm, một đường thẳng hoặc một hình qua phép biến hình.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cùng với các phương pháp giải nhanh chóng, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
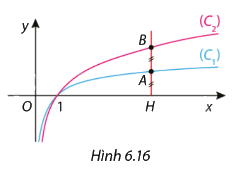
Cho đồ thị của hai hàm số \(y = {\log _a}x\); \(y = {\log _b}x\) lần lượt là (C1) và (C2) (Hình 6.16).
Đề bài
Cho đồ thị của hai hàm số \(y = {\log _a}x\); \(y = {\log _b}x\) lần lượt là (C1) và (C2) (Hình 6.16). Tìm hệ thức liên hệ giữa a và b, biết mọi đường thẳng song song với trục tung, cắt trục hoành, (C1), (C2) lần lượt tại H, A, B thì A là trung điểm của BH.
Phương pháp giải - Xem chi tiết
A là trung điểm của BH nên \({y_B} = 2{y_A}\)
Theo đồ thị trên hình vẽ thì \({x_A} = {x_B} = {x_H}\)
Áp dụng: \({\log _a}b = c \Leftrightarrow {a^c} = b\).
Lời giải chi tiết
Gọi điểm \(H\left( {{x_H};0} \right)\), \(A\left( {{x_A};{y_A}} \right)\), \(B\left( {{x_B};{y_B}} \right)\)
A là trung điểm của BH nên \({y_B} = 2{y_A}\)
Theo đồ thị trên hình vẽ thì \({x_A} = {x_B} = {x_H}\)
Ta có điểm A thuộc (C1) nên \({y_A} = {\log _a}{x_A} \Leftrightarrow {a^{{y_A}}} = {x_A}\)
Điểm B thuộc (C2) nên \({y_B} = {\log _b}{x_B} \Leftrightarrow {b^{{y_B}}} = {x_B} \Leftrightarrow {b^{2{y_A}}} = {x_A}\)
\( \Rightarrow {\left( {{b^2}} \right)^{{y_A}}} = {a^{{y_A}}} \Leftrightarrow {b^2} = a\)
Bài 6.11 trang 19 SGK Toán 11 tập 2 là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về phép biến hình. Để giải bài tập này, chúng ta cần nắm vững các khái niệm cơ bản như:
Nội dung bài tập: Bài 6.11 thường yêu cầu học sinh xác định ảnh của một điểm, một đường thẳng hoặc một hình qua một phép biến hình cụ thể. Ví dụ, cho điểm A(x0, y0) và phép tịnh tiến theo vectơ v = (a, b), hãy tìm tọa độ điểm A' là ảnh của A qua phép tịnh tiến đó.
Để giải bài tập này một cách hiệu quả, chúng ta có thể áp dụng các bước sau:
Ví dụ: Cho điểm A(2, 3) và phép tịnh tiến theo vectơ v = (1, -2). Tìm tọa độ điểm A' là ảnh của A qua phép tịnh tiến đó.
Giải:
Áp dụng công thức phép tịnh tiến, ta có:
x' = x + a = 2 + 1 = 3
y' = y + b = 3 + (-2) = 1
Vậy, tọa độ điểm A' là (3, 1).
Để nắm vững kiến thức và kỹ năng giải bài tập về phép biến hình, bạn nên luyện tập thêm với các bài tập tương tự trong SGK và các tài liệu tham khảo khác. giaitoan.edu.vn cung cấp một kho bài tập phong phú, đa dạng với lời giải chi tiết, giúp bạn tự tin chinh phục các bài toán khó.
Ngoài ra, bạn cũng có thể tham khảo các video hướng dẫn giải bài tập trên YouTube hoặc các trang web học toán online khác. Điều quan trọng là bạn cần hiểu rõ bản chất của các phép biến hình và áp dụng các công thức một cách linh hoạt.
Các bài tập liên quan:
Hy vọng với những hướng dẫn chi tiết trên, bạn đã hiểu rõ cách giải Bài 6.11 trang 19 SGK Toán 11 tập 2. Chúc bạn học tập tốt!