Bài 6.10 trang 19 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 tập 2, tập trung vào việc vận dụng kiến thức về phép biến hình để giải quyết các bài toán cụ thể. Bài tập này đòi hỏi học sinh phải nắm vững các khái niệm về phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cùng với các phương pháp giải bài tập hiệu quả, giúp bạn tự tin chinh phục môn Toán 11.
Tìm hàm số \(y = C.{a^x}\) mà đồ thị của nó được biểu diễn dưới đây:
Đề bài
Tìm hàm số \(y = C.{a^x}\) mà đồ thị của nó được biểu diễn dưới đây:
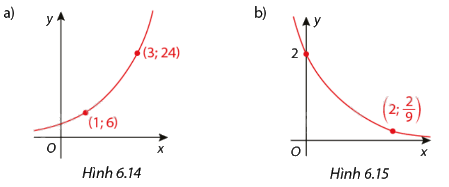
Phương pháp giải - Xem chi tiết
Đồ thị đi qua 2 điểm A(a; b), B (c; d). Thay tọa độ các điểm vào hàm số để tìm C, a.
Lời giải chi tiết
a) Đồ thị hàm số với a >1, đi qua 2 điểm (1; 6) và (3; 24). Ta có:
\(\left\{ \begin{array}{l}C.{a^1} = 6\\C.{a^3} = 24\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}C.a = 6\\C.{a^3} = 24\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}C.a = 6\\{a^2} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}a = 2\\a = - 2\,\left( {\rm{L}} \right)\end{array} \right.\\C.a = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\C = 3\end{array} \right.\)
Vậy hàm số cần tìm là \(y = {3.2^x}\).
b) Đồ thị hàm số với 0 < a < 1, đi qua 2 điểm \(\left( {2;\frac{2}{9}} \right)\) và \(\left( {0;2} \right)\). Ta có:
\(\left\{ \begin{array}{l}C.{a^2} = \frac{2}{9}\\C.{a^0} = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}C.{a^2} = \frac{2}{9}\\C = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{a^2} = \frac{1}{9}\\C = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}a = \frac{1}{3}\\a = - \frac{1}{3}\left( {\rm{L}} \right)\end{array} \right.\\C = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{1}{3}\\C = 2\end{array} \right.\)
Vậy hàm số cần tìm là \(y = 2.{\left( {\frac{1}{3}} \right)^x}\)
Bài 6.10 trang 19 SGK Toán 11 tập 2 yêu cầu học sinh vận dụng kiến thức về các phép biến hình đã học để giải quyết một bài toán cụ thể. Để giải bài toán này một cách hiệu quả, chúng ta cần thực hiện các bước sau:
Đề bài: Trong mặt phẳng tọa độ Oxy, cho điểm A(1; 2). Hãy tìm ảnh A' của điểm A qua phép tịnh tiến theo vectơ v = (3; -1).
Giải:
Áp dụng công thức phép tịnh tiến:
A'(x' ; y') = A(x ; y) + v(a ; b) = (x + a ; y + b)
Thay tọa độ điểm A(1; 2) và vectơ v = (3; -1) vào công thức, ta được:
A'(1 + 3 ; 2 - 1) = A'(4 ; 1)
Vậy, ảnh A' của điểm A qua phép tịnh tiến theo vectơ v = (3; -1) là A'(4; 1).
Để giải nhanh các bài tập về phép biến hình, bạn nên:
Ngoài SGK Toán 11 tập 2, bạn có thể tham khảo thêm các tài liệu sau để học tốt hơn về phép biến hình:
Bài 6.10 trang 19 SGK Toán 11 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về phép biến hình. Bằng cách nắm vững công thức, luyện tập thường xuyên và áp dụng các mẹo giải nhanh, bạn có thể tự tin giải quyết bài tập này một cách hiệu quả. Chúc bạn học tốt!